Регистрация Спросить otvet5GPT
vingers
12.05.2021 00:26
Математика
Есть ответ 👍

Вычислите: 1) 7 и 14пятнадцатых + 2 и 1 пятнадцатая= 2) 9 и 24 двадцать седьмых + 12 и 13 двадцать седьмых = 3) 1- 12 девятнадцатых = 4)8-3 и 6 пятнадцатых = 5)12-11 и 6 одиннадцатых= 6)16 и 3 тринадцатых - 6 и 8 тринадцатых= 7)13 и 4 девятых - 2 и 8 девятых = 8)10
и 7 шестнадцатых - 4 и 12 шестнадцатых= 9)29 и 49 пяттдесят третих - 8 и 49 пятдесят третих = 10) (20 и 16 двадцать пятых + 13 и 9 двадцать ии 4 четырнадцатых+ 7 и тринадцатых).

140
467
Посмотреть ответы 2

Ответы на вопрос:

bubles13
bubles13
4,4(34 оценок)

1) 10 целых

2) 22 целые и 10 двадцать седьмых

3) 7 девятнадцатых

4) не поняла

5) не поняла

6) 9 целыз и 8 тринадцатых

7) 10 и 5 девятых

8) 5 и 11 шестнадцатых

9) 21 целая

10) 34 целых - ?

Diamond1111111
Diamond1111111
4,7(27 оценок)

Пошаговое объяснение:

Пусть парабола имеет вид

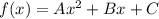f(x) = Ax^2 + Bx + C. (Эти A, B, C не имеют никакого отношения к точкам из условия, просто поздно заметил что выбрал не самые удачные имена для неопределенных коэффициентов).

По условию знаем, что

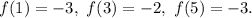
f(1) = -3,\ f(3)=-2,\ f(5)=-3.

Заметим, что 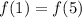f(1) = f(5), это значит, что парабола симметрична относительно прямой 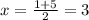x = \frac{1 + 5}{2} = 3. То есть абсцисса вершины параболы равна 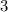3. Что дает нам условие:

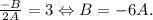
\frac{-B}{2A} = 3 \Leftrightarrow B = -6A.

После этого упрощения наша функция принимает такой вид:

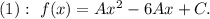
(1):\ f(x) = Ax^2 - 6Ax + C.

Из условия известно: 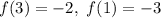f(3) = -2,\ f(1) = -3. Подставим это в выражение (1) и получим систему уравнений:

-2 = -9A + C

-3 = -5A + C

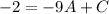
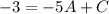
Опуская подробности решения этой простой системы уравнения, получаем

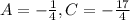A = -\frac{1}{4}, C = -\frac{17}{4}. (Что решение верное легко можно убедиться проверкой).

Вспомним что 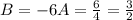B = -6A = \frac{6}{4} = \frac{3}{2}.

То есть парабола имеет вид

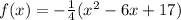f(x) = -\frac{1}{4}(x^2-6x +17). Осталось найти площадь криволинейной трапеции по формуле

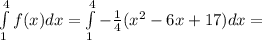
\int\limits_1^4 f(x)dx = \int\limits_1^4 -\frac{1}{4}(x^2 - 6x + 17) dx =

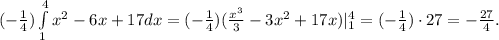
(-\frac{1}{4})\int\limits_1^4x^2 - 6x + 17dx = (-\frac{1}{4})(\frac{x^3}{3} - 3x^2 + 17x)|_1^4 = (-\frac{1}{4})\cdot 27 = -\frac{27}{4}.

Почему площадь получилась с отрицательным знаком? Потому что парабола лежит ниже оси oX, а формула

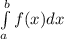\int\limits_a^b f(x)dx дает так называемую ореинтированную площадь (всё что ниже оХ берется со знаком -, всё что выше со знаком +). Таким образом чтобы получить обычную площадь криволинейной трапеции достаточна взять от полученного ответа модуль.

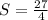
S = \frac{27}{4}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS