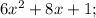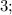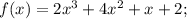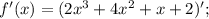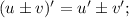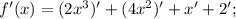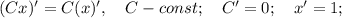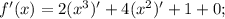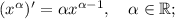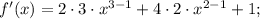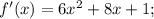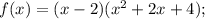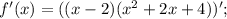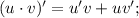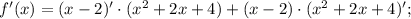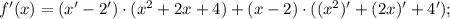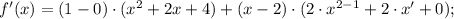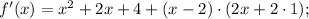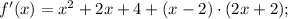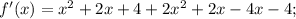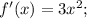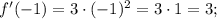знаток Найдите производную f(x) в указанной точке
f'(x), когда f(x)=2x^3 +4x^2+x+2
f'(-1), когда f(x)=(x-2)(x^2+2x+4)
203
458
Ответы на вопрос:
потребуется sбок+sосн;
h=180/(6*10)=3 см;
sбок=2*(6*3)+2*(10*3)+(6*10)=36+60+60=156 см² - тебе потребуется.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
надо решите уравнение...
 AzatDit09.02.2021 22:50
AzatDit09.02.2021 22:50 -
Разложите на множители: (a-c)(a+c) _ (a-b)^2 - (a-b-c)(a-b+c)-4...
 aboderu20.05.2021 00:19
aboderu20.05.2021 00:19 -
Запишите множество корней уравнения |х...
 кристина215621.10.2022 17:37
кристина215621.10.2022 17:37 -
Выполнить действие (2xy^2)d^3)×(-3x^2y^3)^2...
 marivtsan08.11.2022 12:35
marivtsan08.11.2022 12:35 -
У=-5х (в квадрат) +10х+46...
 AnnaVorob199926.03.2022 11:51
AnnaVorob199926.03.2022 11:51 -
В трапеции ABCD градусные меры углов A, B и С относятся к 2:7:8.Найдите...
 FUNNIAO05.10.2021 11:04
FUNNIAO05.10.2021 11:04 -
ДОБРЫЕ ЛЮДИ мне решить это задание определите точки пересечения...
 vasiaplaton07.06.2021 13:15
vasiaplaton07.06.2021 13:15 -
ХЭЛП! Решите как можно подробнее. Заранее...
 dima1tod20.02.2020 21:25
dima1tod20.02.2020 21:25 -
Решите систему уравнений 5x-y=9 3x+4y=10...
 dary09007.03.2021 20:34
dary09007.03.2021 20:34 -
Найдите значение выражения 3а^2,если а=х+2...
 mawa1818.08.2021 05:29
mawa1818.08.2021 05:29

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.