В равнобедренном треугольнике с периметром 57 см основание относится к боковой стороне как 2:3

279

365

Посмотреть ответы 2

Ответы на вопрос:

IvanKabakov

Геометрия

4,6(56 оценок)

Объяснение:

т.к. треугольник равнобедренный, боковые стороны равный, тогда

2х+2х+3х=57

7х=57

х=57:7

х=

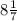
$8 \frac{1}{7}$

Боковые стороны =x×2(посчитайте мне не удобно)

основание =х×3(посчитайте)

nada9999

Геометрия

4,8(35 оценок)

А) ∠аmn=90 °; ∠acn= 90 °. сумма противоположных углов четырехугольника сnma равна 180 °, значит около четырехугольника cnma можно описать окружность. ∠сmn=∠can как вписанные углы, опирающиеся на одну и ту же дугу nc. б) так как точка м– середина гипотенузы является центром окружности, описанной около треугольника авс, то вm=am=cm треугольник cmb – равнобедренный, так как сm=bm. треугольник anb – равнобедренный, так как nm – серединный перпендикуляр к ав, поэтому bn=an. угол в в этих треугольниках общий. по теореме синусов из треугольника аnb bn/sin∠b=2r1, r1– радиус окружности, описанной около треугольника anb. по теореме синусов из треугольника смв: сm/sin ∠b=2r2 r2– радиус окружности, описанной около треугольника смв значит r1/r2=bn/cm, так как см=вм. r1/r2=bn/bm рассмотрим прямоугольный треугольник вnm: cos∠b=bm/bn r1/r2=1/cos∠b по условию tg∠a=4/3 ⇒ 1+tg2∠a=1/cos2∠a значит cos2∠a=1/(1+tg2∠a)=1/(1+(4/3)2)=9/25 так как угол а –острый, то cos∠a=3/5 sin∠a=4/5 sin∠a=cos∠b r1/r2=1/cos∠b=1/(4/5)=5/4 о т в е т. 5/4

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.