Регистрация Спросить otvet5GPT
Helpmeplease1114
05.03.2021 13:28
Математика
Есть ответ 👍

Применяя дифференцирование по параметру вычислинтеграл

плез

179
306
Посмотреть ответы 2

Ответы на вопрос:

ДарьяКаракал
ДарьяКаракал
4,4(16 оценок)

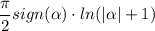
\dfrac{\pi}{2} sign(\alpha)\cdot ln(|\alpha|+1)

Пошаговое объяснение:

На мн-ве 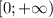[0;+\infty) подынтегральная функция, очевидно, определена везде, кроме точки x=0.

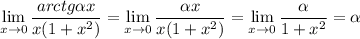
\lim\limits_{x\to 0} \dfrac{arctg \alpha x}{x(1+x^2)}=\lim\limits_{x\to 0} \dfrac{\alpha x}{x(1+x^2)}=\lim\limits_{x\to 0} \dfrac{\alpha }{1+x^2}=\alpha

А тогда, если доопределить подынтегральную функцию в нуле значением 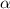\alpha , она станет непрерывной по x на промежутке 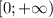[0;+\infty). При этом, очевидно, на значение интеграла такое доопределение не влияет.

По 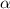\alpha подынтегральная функция, очевидно, непрерывна.

А тогда, согласно теореме о дифференцировании по параметру, получим:

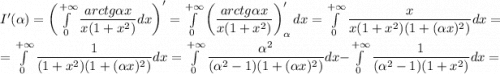
I'(\alpha)=\left(\int\limits_0^{+\infty}\dfrac{arctg \alpha x}{x(1+x^2)}dx\right )'=\int\limits_0^{+\infty}\left(\dfrac{arctg \alpha x}{x(1+x^2)}\right)'_\alpha dx=\int\limits_0^{+\infty}\dfrac{x}{x(1+x^2)(1+(\alpha x)^2)} dx=\\ =\int\limits_0^{+\infty}\dfrac{1}{(1+x^2)(1+(\alpha x)^2)} dx=\int\limits_0^{+\infty}\dfrac{\alpha^2}{(\alpha^2-1)(1+(\alpha x)^2)} dx-\int\limits_0^{+\infty}\dfrac{1}{(\alpha^2-1)(1+x^2)} dx=\\=\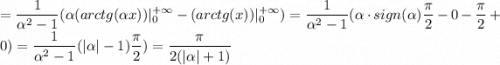dfrac{1}{\alpha^2-1}(\alpha (arctg(\alpha x))|\limits_0^{+\infty}-(arctg(x))|\limits_0^{+\infty})=\dfrac{1}{\alpha^2-1}(\alpha\cdot sign(\alpha)\dfrac{\pi}{2}-0-\dfrac{\pi}{2}+0)=\dfrac{1}{\alpha^2-1}(|\alpha|-1)\dfrac{\pi}{2})=\dfrac{\pi}{2(|\alpha|+1)}

Тогда

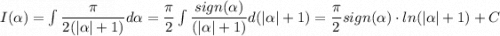
I(\alpha)=\int\dfrac{\pi}{2(|\alpha|+1)}d\alpha=\dfrac{\pi}{2}\int\dfrac{sign(\alpha)}{(|\alpha|+1)}d(|\alpha|+1)=\dfrac{\pi}{2} sign(\alpha)\cdot ln(|\alpha|+1)+C

Очевидно для начального условия взять 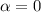\alpha=0:

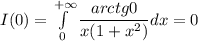
I(0)=\int\limits_{0}^{+\infty} \dfrac{arctg0}{x(1+x^2)}dx=0

А тогда 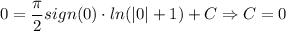0=\dfrac{\pi}{2} sign(0)\cdot ln(|0|+1)+C\Rightarrow C=0

kirkanobotan
kirkanobotan
4,8(18 оценок)
15*3=45 человек в трёх бригадах

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS