BeautifulGirl001

30.11.2021 07:46

Есть ответ 👍

Вычислите периметр треугольника, если вершины треугольника являются пересечениями графика функции y = x²-8 и осей координат!

114

479

Посмотреть ответы 2

Ответы на вопрос:

11912

Математика

4,6(84 оценок)

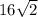
$16\sqrt{2}$

Пошаговое объяснение:

$y=x^{2}-8;$

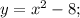
Найдём координаты точек пересечения графика функции с осью абсцисс. Для этого вместо "у" подставим 0:

$x^{2}-8=0;$

$x^{2}=8;$

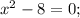
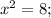
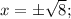
$x=\pm \sqrt{8};$

Имеем две точки:

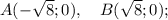
$A(-\sqrt{8}; 0), \quad B(\sqrt{8}; 0);$

Теперь найдём координату точки пересечения графика функции с осью ординат. Для этого вместо "х" подставим 0:

$y=0^{2}-8;$

y=0-8;

y=-8;

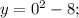
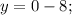
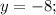
Имеем точку:

C(0; -8);

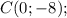
Мы нашли координаты вершин треугольника. Теперь найдём значения сторон треугольника:

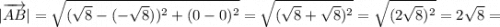
$|\overrightarrow {AB}|=\sqrt{(\sqrt{8}-(-\sqrt{8}))^{2}+(0-0)^{2}}=\sqrt{(\sqrt{8}+\sqrt{8})^{2}}=\sqrt{(2\sqrt{8})^{2}}=2\sqrt{8}=$

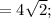
$=4\sqrt{2};$

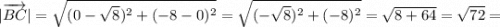
$|\overrightarrow {BC}|=\sqrt{(0-\sqrt{8})^{2}+(-8-0)^{2}}=\sqrt{(-\sqrt{8})^{2}+(-8)^{2}}=\sqrt{8+64}=\sqrt{72}=$

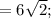
$=6\sqrt{2};$

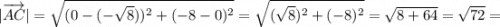
$|\overrightarrow {AC}|=\sqrt{(0-(-\sqrt{8}))^{2}+(-8-0)^{2}}=\sqrt{(\sqrt{8})^{2}+(-8)^{2}}=\sqrt{8+64}=\sqrt{72}=$

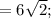
$=6\sqrt{2};$

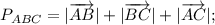
$P_{ABC}=|\overrightarrow {AB}|+|\overrightarrow {BC}|+|\overrightarrow {AC}|;$

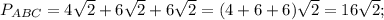
$P_{ABC}=4\sqrt{2}+6\sqrt{2}+6\sqrt{2}=(4+6+6)\sqrt{2}=16\sqrt{2};$

baha50

Математика

4,7(2 оценок)

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.