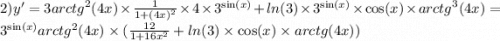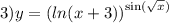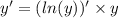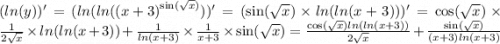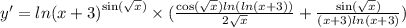Регистрация Спросить otvet5GPT
асем198566
12.03.2021 19:16
Алгебра
Есть ответ 👍

решить. Продифференцировать данные функции:

235
439
Посмотреть ответы 2

Ответы на вопрос:

maruha3008
maruha3008
4,7(64 оценок)

2)y' = 3 {arctg}^{2} (4x) \times \frac{1}{1 + {(4x)}^{2} } \times 4 \times {3}^{ \sin(x) } + ln(3) \times { 3}^{ \sin(x) } \times \cos(x) \times {arctg}^{3} (4x) = {3}^{ \sin(x) } {arctg}^{2} (4x) \times ( \frac{12}{1 + 16 {x}^{2} } + ln(3) \times \cos(x) \times arctg(4x))

3)y = {( ln(x + 3)) }^{ \sin( \sqrt{x} ) }

используем формулу:

y' = ( ln(y))' \times y

(ln(y) )' = ( ln( ln(( {x + 3)}^{ \sin( \sqrt{x} ) } ) )' = ( \sin( \sqrt{x} ) \times ln( ln(x + 3) ) )' = \cos( \sqrt{x} ) \times \frac{1}{2 \sqrt{x} } \times ln( ln(x + 3) ) + \frac{1}{ ln(x + 3) } \times \frac{1}{x + 3} \times \sin( \sqrt{x} ) = \frac{ \cos( \sqrt{x} ) ln( ln(x + 3) ) }{2 \sqrt{x} } + \frac{ \sin( \sqrt{x} ) }{(x + 3) ln(x + 3) }

y' = { ln(x + 3) }^{ \sin( \sqrt{x} ) } \times ( \frac{ \cos( \sqrt{x} ) ln( ln(x + 3) ) }{2 \sqrt{x} } + \frac{ \sin( \sqrt{x} ) }{( x + 3) ln(x + 3) } )

samuraterikov0
samuraterikov0
4,6(70 оценок)
Это обычное квадратное уравнение, оно не имеет корней, когда дискриминант строго меньше нуля, следовательно   3х^2+кх+1=0 д=k^2-12   k^2-12< 0 k^2< 12 k< (12)      ( (  ) - корень ) при к < корня из 12 уравнение не имеет корней. тут получается любое отрицательное число, например -1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS