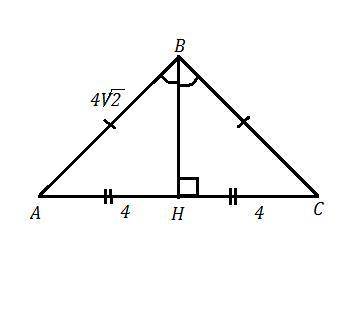
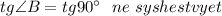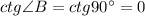Решите уравнения: А) х²-9х+20=0
б) х²+11х-12=0
в) х²+х-56=0
Г) х²-19х+88=0
очень нужно
221
339
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Lg(x^2-2)=-lg1/x решите, . гуманитарий тупит : d...
 м08087801.06.2023 21:24
м08087801.06.2023 21:24 -
Определите,является функция четной или нечетной: y=2sinx-8 x(в 5 степени)...
 miloft18.02.2020 11:51
miloft18.02.2020 11:51 -
Найдите точки экстремума функции y=x^2e^x...
 elinazayka10.01.2021 18:20
elinazayka10.01.2021 18:20 -
Найти значение выражения. 1)42/2^log(2)3 2)6^log(36)16 3)log(5)корень...
 ser200312318.01.2021 20:27
ser200312318.01.2021 20:27 -
Определите точки пересечения графика с координатами осями ox и oy(если...
 beyn1oyc4cd12.07.2022 12:00
beyn1oyc4cd12.07.2022 12:00 -
Найти площадь сферы, диаметр которой равен 6, пологая п=3,14...
 filip19858521.07.2021 19:07
filip19858521.07.2021 19:07 -
При каких значениях p дробь корень из p-1/p-1 принимает наибольшее значение?...
 гребок24.12.2022 23:33
гребок24.12.2022 23:33 -
Решите систему: x^2=2y+3; x^2+6=2y+y^2)...
 nsotskova18.05.2021 17:07
nsotskova18.05.2021 17:07 -
Решите с уравнения брат в 2 раза старше сестры. сколько лет сестре и...
 M4KAR14.06.2023 00:53
M4KAR14.06.2023 00:53 -
Представьте данный одночлен в виде куба одночлена: а)-64m^9n^21; б)-2...
 lolii0ikolik07.09.2020 05:19
lolii0ikolik07.09.2020 05:19

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

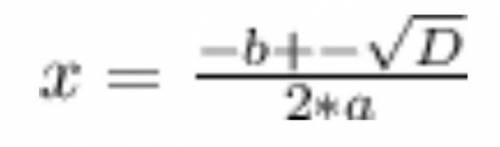
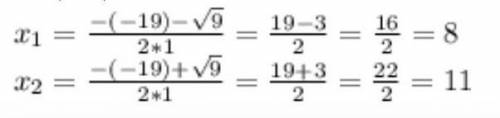

![\Big[\ cos\angle B=\Big(\dfrac{\sqrt2}{2}\Big)^2-\Big(\dfrac{\sqrt2}{2}\Big)^2=0\ \Big]](/tpl/images/4081/6890/47bb5.png)