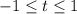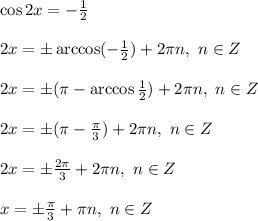Выразите у через х в уравнении 6х — 12у + 1,8 = 0 A) у=0,5х-0,3
B) у=-0,5х+0,3
C) у=0,5х+0,3
D) у=2х +3
E) у=0,5х+0,15
185
456
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Вартість деякого товару 80 грн.Спочатку його вартість збильшили на 10%...
 Neznаykа26.02.2021 02:10
Neznаykа26.02.2021 02:10 -
A-b =43 120a+18b = -110 Решить систему...
 avatariyaflora25.01.2022 02:59
avatariyaflora25.01.2022 02:59 -
Для приготовления цементного раствора берут 1 часть цемента, 3 части песка...
 Teroristka12302.12.2021 19:48
Teroristka12302.12.2021 19:48 -
в корзине 4 шара, красный, синий, черный и трехцветный. найдите вероятность...
 Lik2037212.06.2023 05:02
Lik2037212.06.2023 05:02 -
Вычисли. 7 РАБОТА В ГРУППЕ 964 800 : (30 - 16) — 14 - 131 57 892:41 - 4...
 ляпрпммм12.03.2020 09:46
ляпрпммм12.03.2020 09:46 -
Спростити вираз 18a+4a-2a...
 Uspex1111112.12.2020 19:16
Uspex1111112.12.2020 19:16 -
найдите наименьшее натуральное число которое при деления на 7 даёт остаток...
 squarenq17.12.2022 06:58
squarenq17.12.2022 06:58 -
Сор по каз яз 5 класс 2 четверть 1 сор...
 nbolshakova115.02.2022 14:41
nbolshakova115.02.2022 14:41 -
5 класс. нужно по быстрее ответ. после 10 минут не беру даже правильные...
 dinbili427.06.2022 21:49
dinbili427.06.2022 21:49 -
Угол DNK равен 136 градусов, луч NEт-биссектриса угла DNK, NF - биссектриса...
 MikiMio26.12.2021 17:11
MikiMio26.12.2021 17:11

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

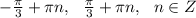
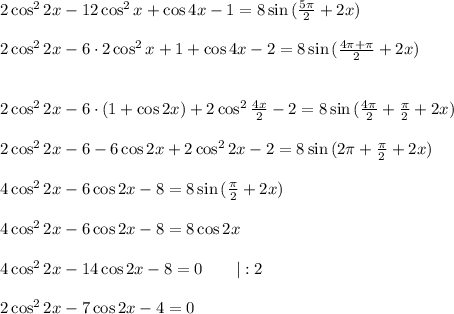
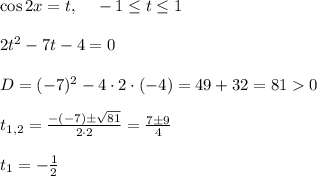
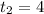 -не подходит, так как
-не подходит, так как