Дана прямая, уравнение которой 3x−2y+12=0. Найди координаты точек, в которых эта прямая пересекает оси координат.

1. Координаты точки пересечения с Ox:
(_;_)

2. Координаты точки пересечения с Oy:
(_;_)

226

356

Посмотреть ответы 2

Ответы на вопрос:

topgaimer

Алгебра

4,8(66 оценок)

Приведем уравнение к виду y = kx + m

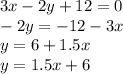
$3x-2y+12=0\\-2y=-12-3x\\y=6+1.5x\\y=1.5x+6$

Теперь делаем таблицу

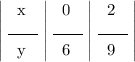
$\left|\;{\begin{array}{}\;\;x\\\line(1,0)9\line(1,0)9\\\;\;y\end{array}\;\right|\left\begin{array}{}\;\;0\\\line(1,0)9\line(1,0)9\\\;\;6\end{array}\;\right|\left\begin{array}{}\;\;2\\\line(1,0)9\line(1,0)9\\\;\;9\end{array}\;\right|$

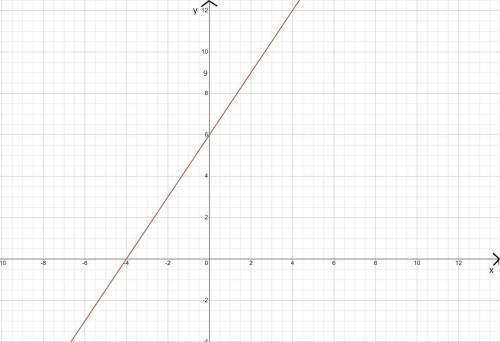
Строим график (см. приложение)

Прямая пересекает точки (0; 6) и (2; 9), график верный

По нему видим, что прямая пересекает ось Ox в точке (-4; 0)

Ось Oy в точке (0; 6)

1. Координаты точки пересечения с Ox: (-4; 0)

2. Координаты точки пересечения с Oy: (0; 6)

Дана прямая, уравнение которой 3x−2y+12=0. Найди координаты точек, в которых эта прямая пересекает о

Vadim55554

Алгебра

4,8(32 оценок)

Так как ak - биссектриса, то: при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки: ищем длины ab и ac: используем формулу: находим координаты точки k: теперь определим вид треугольника для этого используем теорему косинусов: для начала найдем длину bc: вид треугольника будем определять по косинусу самого большого угла; если cos< 0, то угол тупой; если cos=0, то угол прямой; если cos> 0, то угол острый. против большей стороны лежит больший угол, поэтому запишем теорему косинусов для ac и косинуса угла b подставим значения: cosb< 0 поэтому угол тупой и треугольник тупоугольный ответ: треугольник тупоугольный

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.