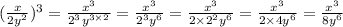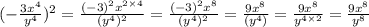Алгебра: Возведите в степень (x/2y^2)^3 (-3x/y4)

Женя3725

06.01.2023 05:54

Алгебра

Есть ответ 👍

Возведите в степень
(x/2y^2)^3
(-3x/y4)

231

461

Посмотреть ответы 2

Ответы на вопрос:

Alisa1Karimova

Алгебра

4,5(51 оценок)

$( \frac{x}{2y {}^{2} } ) {}^{3} = \frac{x {}^{3} }{2 {}^{3{}^{} }y {}^{3 \times 2} } = \frac{x {}^{3} }{2 {}^{3} y {}^{6} } = \frac{x {}^{3} }{2 \times 2 {}^{2} y {}^{6} } = \frac{x {}^{3} }{2 \times 4y {}^{6} } = \frac{ {x}^{3} }{8y {}^{6} }$

$( - \frac{3x {}^{4} }{y {}^{4} } ) {}^{2} = \frac{( - 3) {}^{2}x {}^{2 \times 4} }{(y {}^{4}) {}^{2} } = \frac{( - 3) {}^{2}x {}^{8}}{(y {}^{4} ) { }^{2} } = \frac{9x {}^{8} }{(y {}^{4} )} = \frac{9x {}^{8} }{y {}^{4 \times 2} } = \frac{9x {}^{8} }{y {}^{8} }$

5867389576M

Алгебра

4,5(26 оценок)

F(x) = 1/3 x³ - x² - 3x +9 x0 = -1 промежуток [-3, 0] а) написать уравнение касательной б) промежутки монотонности и экстремумы в) наибольшее и наименьшее значение функции на указанном промежутке. решаем. производная = х² - 2х - 3 х² - 2х - 3 = 0 ( ищем точки экстремумов) по т. виета х1 = 3 и х2 = -1 -∞ + -1 - 3 + +∞ это знаки производной возрастает убывает возрастает х = -1 - это точка максимума х = 3 - это точка минимума в промежуток [-3, 0] попадает только точка х = -1 считаем: х = -1 f(-1) = 1/3·(-1)³ )² - 3·(-1) + 9 = -1/3 -1 +3 +9 = 10 2/3 ( наибольшее значение) х = -3 f(-3) = 1/3·(-3)³ )² -3·(-3) + 9 = -9 -9 +9 +9 = 0 (наименьшее значение) х = 0 f(0) = 9

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.