Спутник был запущен в 5 часов29минут 42 секунды и вышел на заданную орбиту через 2 часа 34 минуты 53 секунды.в котором часу это произошло?
Ответы на вопрос:
5ч 29мин 42 сек+2ч 34 мин 53 сек=1)5ч+2ч=7ч, 2)29мин+34мин=63мин(1ч 3 мин), 3)42сек+53сек=95сек(1мин 35 сек), 4)7ч+1ч+3мин+1мин+35сек=в 8ч 04 мин 35 сек.-это произошло.
все легко сначало считаем секунды : 42+53=95 секуннд=1 минута 35секунд
потом минуты: 29+34=63 и + 1 минута из остатка секунд и того 64 мин=1 ч 4 минуты
и послетнее часы 5+2=7 и остаток +1час =8ч4минутыи 35 секунд
а) 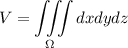 . В нашем случае
. В нашем случае 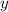 меняется от
меняется от 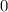 до
до 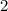 ,
,  меняется от
меняется от 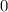 до
до 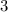 , а
, а  заключен между
заключен между 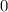 и
и 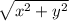 . По сути
. По сути  можно представлять себе как множество отрезков высоты
можно представлять себе как множество отрезков высоты 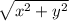 выпущенных из точки
выпущенных из точки 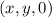 , причем эти точки берутся из прямоугольника
, причем эти точки берутся из прямоугольника ![[0,2]\times [0,3]](/tpl/images/4758/9834/e2d7a.png) .
.
Итак, 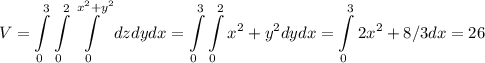 .
.
б) Здесь рассуждения такие же, только  представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости
представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости 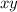 . Величина
. Величина  будет меняться от
будет меняться от 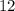 до минимального значения на
до минимального значения на  , что соответствует максимуму
, что соответствует максимуму 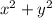 на
на  -- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке
-- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке 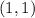 (а начало координат не подходит). Значит,
(а начало координат не подходит). Значит, 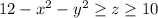 . Итого:
. Итого: 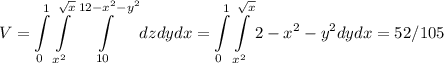 .
.
в) Здесь удобно сделать замену координат: 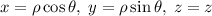 , тогда поверхности:
, тогда поверхности: 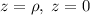 . Якобиан
. Якобиан 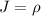 , имеем:
, имеем: 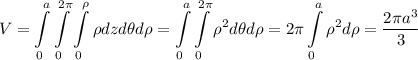 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Реши уравнение 2х+3=0...
 Осьминог1318.08.2021 20:59
Осьминог1318.08.2021 20:59 -
8. Найдите площадь фигуры. нужно ...
 ichmaelz17.02.2020 09:28
ichmaelz17.02.2020 09:28 -
3. Вычисли. Проверь. Сравни значения выражений ва и б. Сделай вывод....
 Goshavasa06.05.2022 16:38
Goshavasa06.05.2022 16:38 -
6. Қарындаштарды қораптарға бөліп салуға көмектес. а) Қораптың санын...
 twilightsun9023.05.2020 20:21
twilightsun9023.05.2020 20:21 -
Одна сторона, которая образует прямой угол прямоугольного треугольника...
 mement0m0ri12.03.2021 06:23
mement0m0ri12.03.2021 06:23 -
Два работника совместно выполняют работу за 4 дня. Если 1-й день...
 matveyking1234511.02.2020 20:14
matveyking1234511.02.2020 20:14 -
Раскройте скобки: а) – 3,2 ∙ (2х + 1,5); б) (4,6у – 5,3) ∙ (- 5)...
 алина388209.11.2021 13:00
алина388209.11.2021 13:00 -
9. Составь задачи по следующим выражениям: 1) 4×6 +3×9; 2) (3 + 5)×2;...
 linashilova0012.03.2023 22:15
linashilova0012.03.2023 22:15 -
Найдите число: 12% которого равно 75...
 kseniiazueva9317.05.2023 21:03
kseniiazueva9317.05.2023 21:03 -
Якою кiлькiстю способiв з колоди в 36 карт можно вибрати невпорядкований...
 lidiyamartin921.08.2020 19:37
lidiyamartin921.08.2020 19:37

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
