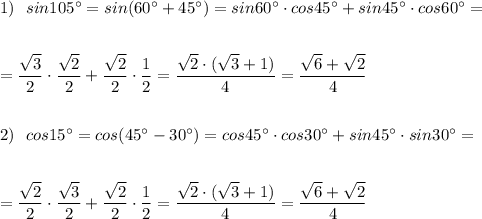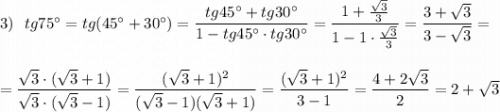Вычислите, представив угол в виде суммы или разности:
sin105°
cos15°
tg75°

186

413

Посмотреть ответы 3

Ответы на вопрос:

Poznavatel01

Алгебра

4,4(21 оценок)

решение на фотографии

Вычислите, представив угол в виде суммы или разности: sin105° cos15° tg75°

XaMeJIuoH

Алгебра

4,8(16 оценок)

$1)\ \ sin105^\circ =sin(60^\circ +45^\circ )=sin60^\circ \cdot cos45^\circ +sin45^\circ \cdot cos60^\circ =\\\\\\=\dfrac{\sqrt3}{2}\cdot \dfrac{\sqrt2}{2}+\dfrac{\sqrt2}{2}\cdot \dfrac{1}{2}=\dfrac{\sqrt2\cdot (\sqrt3+1)}{4}=\dfrac{\sqrt6+\sqrt2}{4} \\\\\\2)\ \ cos15^\circ =cos(45^\circ -30^\circ )=cos45^\circ \cdot cos30^\circ +sin45^\circ \cdot sin30^\circ =\\\\\\=\dfrac{\sqrt2}{2}\cdot \dfrac{\sqrt3}{2}+\dfrac{\sqrt2}{2}\cdot \dfrac{1}{2}=\dfrac{\sqrt2\cdot (\sqrt3+1)}{4}=\dfrac{\sqrt6+\sqrt2}{4}$

$3)\ \ tg75^\circ =tg(45^\circ +30^\circ )=\dfrac{tg45^\circ +tg30^\circ }{1-tg45^\circ \cdot tg30^\circ }=\dfrac{1+\frac{\sqrt3}{3}}{1-1\cdot \frac{\sqrt3}{3}}=\dfrac{3+\sqrt3}{3-\sqrt3}=\\\\\\=\dfrac{\sqrt3\cdot (\sqrt3+1)}{\sqrt3\cdot (\sqrt3-1)}=\dfrac{(\sqrt3+1)^2}{(\sqrt3-1)(\sqrt3+1)}=\dfrac{(\sqrt3+1)^2}{3-1}=\dfrac{4+2\sqrt3}{2}=2+\sqrt3$

rrrf1

Алгебра

4,8(65 оценок)

${(\frac{69 + 56}{5}) }^{3} = {25}^{3} = 15625 - (69 \times 56) = 11761$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Ruda05
08.01.2023 22:44

Решение с объяснением. решите неравенство: а) 0,2х(х-1)-х(0,2х+0,5)...
artem110616
29.03.2023 19:14

Основное свойство дроби. что называется сокращениям дробей?...
ailchencko2010
11.06.2021 14:49

Найти наименьшее значение функции: y=(x+4)^2(x+10)+9 на отрезке...
11516118
26.01.2021 02:29

1)решить неравенства : |х-1| 3,4 ; |4х-0,8|≥2. 2)решить неравенство:...
sofyaoborina12
25.02.2022 15:55

1. решите уравнение: а) 3 1 x = 12; б) 6x - 10,2 = 0; в) 5x...
PaFaS123
28.08.2020 11:44

Не получается решить. x^6 - 3x^5 + 2x^4 - x^2 + 3x - 2 = 0 получается,...
oleksandrskorbat
19.01.2021 13:22

Составить уровнение по : у коли и пети 98 марок, причём у коли...
milanareemets
23.02.2021 22:41

Решить уравнение с решением 3(2x-4)-x=-5...
elveranasibull
19.11.2021 05:26

График функции y = -2x + b проходит через a найдите b если а)...
там12
22.03.2023 16:27

Счастья тому кто : 3 найдите область значения функции у=х2-4х-13...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.