Регистрация Спросить otvet5GPT
aneechkaa000
09.07.2021 07:47
Алгебра
Есть ответ 👍

Контрольная работа по теме «Функции и их свойства. Квадратный трехчлен» Вариант №1.
1. Функция задана формулой f(x)= 2х^2-3.
Найдите: а) f (-1); б) f (0); в) f (2).
2. Функция задана формулой f(x)= 5x-7.
Найдите значение хпри котором: а)f(x)= 3; б)f(x)= -6|
3. Найдите корни квадратного трехчлена:
а) x^2+2х-8=0; б) 5x^2 -9х-2=0; в) 2х^2 -8=0.
4. Разложите на множители квадратный трехчлен:
а) 3х^2-7х+2=0; в) х^2+бх-7=0.
5. По графику функции определить:
а) область определения функции;
y
б) область значений функции;
в) промежутки возрастания функции;
г) промежутки убывания функции;
д) нуди функции;
е) промежутки на которых функция
принимает положительные значения;
0
х) промежутки на которых функция
принимает отрицательные значения;
3) наибольшее и наименьшее значение
функции.​

131
265
Посмотреть ответы 1

Ответы на вопрос:

ученица2002222
ученица2002222
4,4(53 оценок)

Пользуемся формулами приведения , формулами суммы и разности тригонометрических функций .

\boxed {\ sin(\alpha \pm \beta )=sin\alpha \, cos\beta \pm cos\alpha \, sin\beta \ }boxed{\ cos(\alpha \pm \beta )=cos\alpha \, cos\beta \mp sin\alpha \, sin\beta \ }

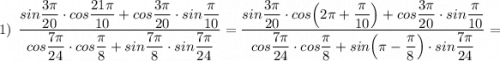
\displaystyle 1)\ \ \frac{sin\dfrac{3\pi}{20}\cdot cos\dfrac{21\pi }{10}+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\dfrac{7\pi}{8}\cdot sin\dfrac{7\pi }{24}}=\frac{sin\dfrac{3\pi}{20}\cdot cos\Big(2\pi +\dfrac{\pi }{10}\Big)+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\Big(\pi -\dfrac{\pi}{8}\Big)\cdot sin\dfrac{7\pi }{24}}=

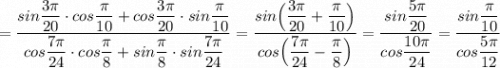
= \dfrac{sin\dfrac{3\pi}{20}\cdot cos\dfrac{\pi }{10}+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\dfrac{\pi}{8}\cdot sin\dfrac{7\pi }{24}}=\dfrac{sin\Big(\dfrac{3\pi}{20}+\dfrac{\pi}{10}\Big)}{cos\Big(\dfrac{7\pi }{24}-\dfrac{\pi}{8} \Big)}=\dfrac{sin\dfrac{5\pi}{20}}{cos\dfrac{10\pi}{24}}=\dfrac{sin\dfrac{\pi}{10}}{cos\dfrac{5\pi}{12}}

Значения 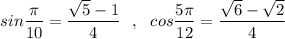  sin\dfrac{\pi }{10}=\dfrac{\sqrt5-1}{4}\ \ ,\ \ cos\dfrac{5\pi }{12}=\dfrac{\sqrt6-\sqrt2}{4}  , тогда в результате

получим 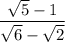   \dfrac{\sqrt5-1}{\sqrt6-\sqrt2}  .

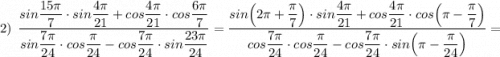
\displaystyle 2)\ \ \frac{sin\dfrac{15\pi}{7}\cdot sin\dfrac{4\pi }{21}+cos\dfrac{4\pi}{21}\cdot cos\dfrac{6\pi}{7} }{sin\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\dfrac{23\pi }{24}}=\frac{sin\Big(2\pi +\dfrac{\pi}{7}\Big)\cdot sin\dfrac{4\pi }{21}+cos\dfrac{4\pi}{21}\cdot cos\Big(\pi -\dfrac{\pi}{7}\Big)}{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\Big(\pi -\dfrac{\pi }{24}\Big)}=

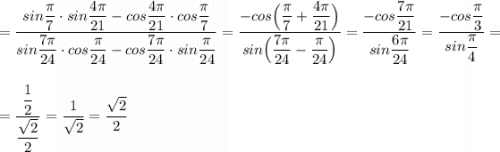
=\dfrac{sin\dfrac{\pi}{7}\cdot sin\dfrac{4\pi }{21}-cos\dfrac{4\pi}{21}\cdot cos\dfrac{\pi}{7} }{sin\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\dfrac{\pi }{24}}=\dfrac{-cos\Big(\dfrac{\pi}{7}+\dfrac{4\pi}{21}\Big)}{sin\Big(\dfrac{7\pi }{24}-\dfrac{\pi}{24}\Big)}=\dfrac{-cos\dfrac{7\pi}{21}}{sin\dfrac{6\pi}{24}}=\dfrac{-cos\dfrac{\pi}{3}}{sin\dfrac{\pi}{4}}==\dfrac{\dfrac{1}{2}}{\dfrac{\sqrt2}{2}} =\dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS