Ответы на вопрос:
Для начала замечу, что под знак корня входит и логарифм. поэтому я обязан наложить следующие ограничения: кроме того, отсюда же следует ограничение и на параметр: . теперь преобразую подкоренное выражение таким образом: вспоминаем теперь о том, что корень чётной степени имеет смысл, если его подкоренное выражение неотрицательно, то есть, отсюда следует неравенство для решения этого неравенства используем метод рационализации(все необходимые ограничения мы уже наложили ранее): теперь необходимо исследовать полученное неравенство. решаем его методом интервалов: отсюда уже видим: 1)пусть . тогда здесь возникают следующие подслучаи(в зависимости от расположения точек x = 8 и x = a на числовой оси): а) тогда неравенство решением имеет отрезок очевидно, условие x > 0 для данного отрезка выполняется(поскольку, очевидно, в этом случае x > 8) и икс отличен от 1(по такой же причине). то есть, в этом случае область определения функции состоит только из указанного отрезка. чтобы в неём лежало ровно 7 целых точек необходимо, чтобы . правый конец не включаем, поскольку при a = 15 в области определения будет лежать и восьмая целая точка. б)пусть теперь , а с учётом рассматриваемых а, . тогда точка x = 8 лежит правее точки x = a и решение неравенства будет иметь вид: . проверим выполнение остальных условий на данном отрезке. поскольку , то заведомо. оба ограничения здесь выполняются, а потому указанный отрезок и есть область определения нашей функции. очевидно, что ровно 7 точек на данном отрезке будут лишь, когда a ∈ . правый конец обязан входить, а вот левый обязан не входить, поскольку иначе на отрезке будет 8 целых точек. поскольку все эти значения больше 1, то эти интервалы пойдут в ответ. в)пусть теперь . тогда получаем неравенство , которое, очевидно, выполняется лишь в одной точке(x = 8). значит, a = 8 условию не удовлетворяет. 2)пусть . тогда и неравенство преобразуется так: ясно, что случай a < 1 нас не устраивает вообще, поскольку неравенство будет иметь своими решениями лишь бесконечные интервалы и обеспечить наличие ровно 7 точек в области определения функции точно не удастся. 3)пусть . тогда a - 1 = 0 и неравенство имеет вид в этом случае неравенство выполняется для любых x. ситуация та же самая. обеспечить наличие в точности 7 точек в области определения мы не сможем. поэтому ответ такой: ∈ ∪
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Спримерами! найдите область определения: ..фото ниже↓...
 teaonline11.05.2020 23:25
teaonline11.05.2020 23:25 -
На рисунке 63 изображён участок земли в форме квадрата .выполнив необходимое...
 amalia20003023.03.2020 21:49
amalia20003023.03.2020 21:49 -
! найдите соотношение сторон треугольника выраженное трёхзначными...
 paatalizip08mh216.11.2021 21:59
paatalizip08mh216.11.2021 21:59 -
, ЕСЛИ Я ВАМ ДАМ ЛУЧШИЙ ОТВЕТ...
 NASRETDINOV110.07.2022 05:07
NASRETDINOV110.07.2022 05:07 -
АЛГЕБРА КОНТРОЛНАЯ 7 КЛАСС...
 Bayu141021.07.2021 14:10
Bayu141021.07.2021 14:10 -
= 6. a) x2 - y? 6) 81 – m2 B) p8 – 49 1) 4a? - 9b2...
 ЯнчикИлИоДуванчик08.11.2020 03:17
ЯнчикИлИоДуванчик08.11.2020 03:17 -
Алгебра тригонометрия побыстрее 1)Вычислить 18cos 5a/2 * cos a/2 если...
 НадеждаКрасюкова21.07.2022 06:47
НадеждаКрасюкова21.07.2022 06:47 -
Записать выражения для нахождения: 1)расстояния (в километрах), пройденного...
 dimas19420.12.2022 16:40
dimas19420.12.2022 16:40 -
Представьте в виде степени: (а^12: а^7)•а^2...
 labzaekaterina05.04.2022 14:48
labzaekaterina05.04.2022 14:48 -
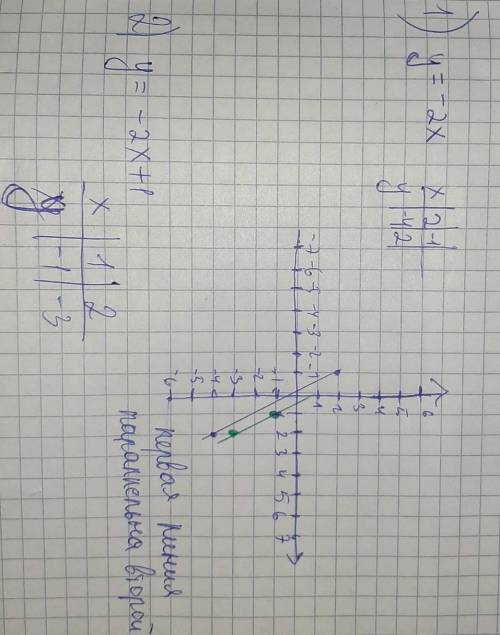
А) постройте график функции у = 3х - 2. б) определите, проходит ли...
 синийлис104.08.2021 19:00
синийлис104.08.2021 19:00

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.