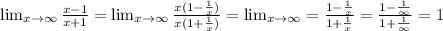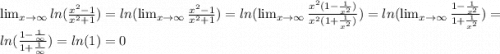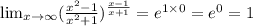Lim x -> бесконечность ((x^2-1)/(x^2+1))^((x-1)/(x+1)) через формулу lim f (x)^g(x)=e^lim g(x) ln f(x)

257

474

Посмотреть ответы 2

Ответы на вопрос:

Дора18119

Математика

4,5(17 оценок)

$\lim_{x \to \infty }( \frac{ {x}^{2} - 1}{ {x}^{2} + 1} ) {}^{ \frac{x - 1}{x + 1} } =\lim_{x \to \infty } {e}^{ ln(( \frac{ {x}^{2} - 1}{ {x}^{2} + 1} ) {}^{ \frac{x - 1}{x + 1} } ) } = {e}^{ \lim_{x \to \infty } \frac{x - 1}{x + 1} ln( \frac{ {x}^{2} - 1}{ {x}^{2} + 1} ) } = {e}^{ \lim_{x \to \infty }( \frac{x - 1}{x + 1}) \lim_{x \to \infty }( ln( \frac{ {x}^{2} - 1 }{ {x}^{2} + 1} ) )}$

Вычислим пределы по-отдельности:

$\lim_{x \to \infty } \frac{x - 1}{x + 1} = \lim_{x \to \infty } \frac{x(1 - \frac{1}{x} )}{x(1 + \frac{1}{x}) } = \lim_{x \to \infty } = \frac{1 - \frac{1}{x} }{1 + \frac{1}{x} } = \frac{1 - \frac{1}{ \infty } }{1 + \frac{1}{ \infty } } = 1$

$\lim_{x \to \infty } ln( \frac{ {x}^{2} - 1 }{ {x}^{2} + 1 } ) = ln( \lim_{x \to \infty } \frac{ {x}^{2} - 1}{ {x}^{2} + 1} ) = ln( \lim_{x \to \infty } \frac{ {x}^{2}(1 - \frac{1}{ {x}^{2} } ) }{ {x}^{2}(1 + \frac{1}{ {x}^{2} } )} ) = ln( \lim_{x \to \infty } \frac{1 - \frac{1}{ {x}^{2} } }{1 + \frac{1}{ {x}^{2} } } ) = ln( \frac{1 - \frac{1}{ \infty } }{1 + \frac{1}{ \infty } } ) = ln(1) = 0$

Собираем:

$\lim_{x \to \infty }( \frac{ {x}^{2} - 1}{ {x}^{2} + 1} ) {}^{ \frac{x - 1}{x + 1} } = {e}^{1 \times 0} = {e}^{0} = 1$

ответ: 1

Лисана539

Математика

4,5(50 оценок)

какой класс? вот,например решение.

треугольник авс - прямоугольный, т к ab²+bc²=ac²

сечение шара плоскостью треугольника окружность, описанная вокруг треугольника, т к на поверхности шара даны три точки а, в, с.

центр описанной окружности - лежит в середине гипотенузы

значит радиус r=ac/2=17/2

на расстоянии от верхней точки шара до плоскости радиус равен 17/2

тогда (r-√35/2)/8,5=r/r

r=8,5+√35/2

объем шара v=4πr³/3=4π(8,5+√35/2)³/2=3008,6π см³

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.