Алгебра: Решите пример, желательно с фоткой

Характеристический многочлен матрицы 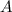есть (не привожу его вычисление здесь, это весьма тривиально): 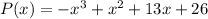. Теорема Гамильтона-Кэли говорит, что 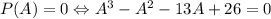. То есть 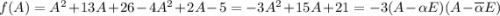, где 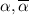-- корни многочлена 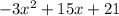. Имеем: 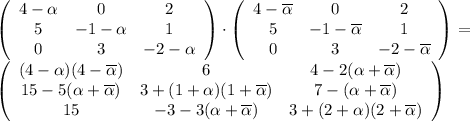. При этом 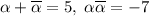, а потому ....

wsmol

04.03.2020 17:30

Алгебра

Есть ответ 👍

Решите пример, желательно с фоткой

260

314

Посмотреть ответы 1

Ответы на вопрос:

PrinssesBublGum1337

Алгебра

4,8(46 оценок)

Характеристический многочлен матрицы есть (не привожу его вычисление здесь, это весьма тривиально): P(x) = -x^3+x^2+13x+26 . Теорема Гамильтона-Кэли говорит, что $P(A) = 0 \Leftrightarrow A^3-A^2-13A+26 = 0$ . То есть $f(A) = A^2+13A+26-4A^2+2A-5 = -3A^2+15A+21 = -3(A-\alpha E)(A-\overline{\alpha}E)$ , где $\alpha,\overline{\alpha}$ -- корни многочлена -3x^2+15x+21 . Имеем: $\left(\begin{array}{ccc}4-\alpha&0&2\\5&-1-\alpha&1\\0&3&-2-\alpha\end{array}\right)\cdot \left(\begin{array}{ccc}4-\overline{\alpha}&0&2\\5&-1-\overline{\alpha}&1\\0&3&-2-\overline{\alpha}\end{array}\right) =\\\left(\begin{array}{ccc}(4-\alpha)(4-\overline{\alpha})&6&4-2(\alpha+\overline{\alpha})\\15-5(\alpha+\overline{\alpha})&3+(1+\alpha)(1+\overline{\alpha})&7-(\alpha+\overline{\alpha})\\15&-3-3(\alpha+\overline{\alpha})&3+(2+\alpha)(2+\overline{\alpha})\end{array}\right)$ . 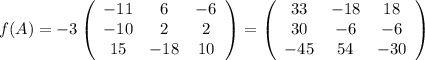При этом $\alpha+\overline{\alpha} = 5,\;\alpha\overline{\alpha}=-7$ , а потому $f(A) = -3\left(\begin{array}{ccc}-11&6&-6\\-10&2&2\\15&-18&10\end{array}\right) = \left(\begin{array}{ccc}33&-18&18\\30&-6&-6\\-45&54&-30\end{array}\right)$ .

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Violettik2006
14.01.2020 03:01

Представьте в виде многочлена:...
крисс1233
02.02.2020 10:45

Построить график у =| sin x - 0,5 |...
jlenabalkinaoyqk93
13.11.2022 08:47

Cos^6+sin^6-sin^2*cos^2 упростить...
lenadub
04.08.2022 02:49

Упростите выражение: sin8а*cos3a - cos8a*sin3a a - это альфа Очень надо...
Lrins
26.08.2022 00:15

Решите уравнение введением новой переменной (x^2+3x+3)(x^2+3x+1)+1=0...
vladus20012
26.12.2021 20:09

Решите уравнение (a+10)a+(5−a)(5+a)=0 В ответ напишите сумму корней, если...
Pomogashka2002
16.03.2020 07:34

Приведите подробные члены многочлены: 6mn-5m²n²-9mn²-11mn +10mn²+5m²n²...
arsigonin
30.06.2020 22:36

Знайти значення добутку f(1)•g( 3), якщо f(х) = х2+4, g(х)= 2х +1....
Kamila28032001
31.03.2020 23:38

Какая точка принадлежит график функции y=2x+1 а) (-4;9). б) (4;9). в)...
Arina0557
21.10.2020 17:22

8. Яка пара чисел є розв язком системи рівнянь x+y-4=0 2x-y+1=0 A. (2;...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.