Регистрация Спросить otvet5GPT
aaaaaaggghhh
25.01.2023 01:58
Математика
Есть ответ 👍

Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. Найти общее решение. 2y'' -y' -y = 4e^(-x/2)

165
467
Посмотреть ответы 2

Ответы на вопрос:

tinita15
tinita15
4,5(16 оценок)

Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену 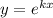y=e^{kx}.

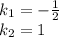
k_1=-\frac{1}{2}\\ k_2=1

Общее решение однородного диф. уравнения: 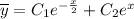\overline{y}=C_1e^{-\frac{x}{2}}+C_2e^x.

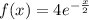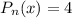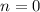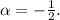Рассмотрим функцию f(x)=4e^{-\frac{x}{2}}. Здесь P_n(x)=4, где n=0, \alpha =-\frac{1}{2}. Сравнивая 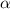\alpha с корнями характеристического уравнения и принимая во внимая, что

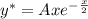
y^*=Axe^{-\frac{x}{2}}

Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на 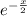e^{-\frac{x}{2}}.

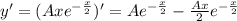
y'=(Axe^{-\frac{x}{2}})'=Ae^{-\frac{x}{2}}-\frac{Ax}{2}e^{-\frac{x}{2}}

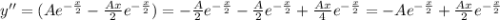
y''=(Ae^{-\frac{x}{2}}-\frac{Ax}{2}e^{-\frac{x}{2}})=-\frac{A}{2}e^{-\frac{x}{2}}-\frac{A}{2}e^{-\frac{x}{2}}+\frac{Ax}{4}e^{-\frac{x}{2}}=-Ae^{-\frac{x}{2}}+\frac{Ax}{2}e^{-\frac{x}{2}}

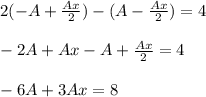
2(-A+\frac{Ax}{2})-(A-\frac{Ax}{2})=4\\ \\ -2A+Ax-A+\frac{Ax}{2}=4\\ \\ -6A+3Ax=8

Приравниваем коэффициенты при степенях x

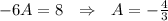
-6A=8~~\Rightarrow~~ A=-\frac{4}{3}

Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения

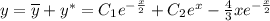
y=\overline{y}+y^*=C_1e^{-\frac{x}{2}}+C_2e^x-\frac{4}{3}xe^{-\frac{x}{2}}

хорошистка552
хорошистка552
4,5(74 оценок)

a

я думаю так. Это тест да?

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS