Геометрия: с контрольной работой!

archakova65

08.02.2023 03:50

Геометрия

Есть ответ 👍

с контрольной работой!

128

188

Посмотреть ответы 2

Ответы на вопрос:

dilfuza2105

Геометрия

4,8(89 оценок)

Объяснение:

Вариант 1

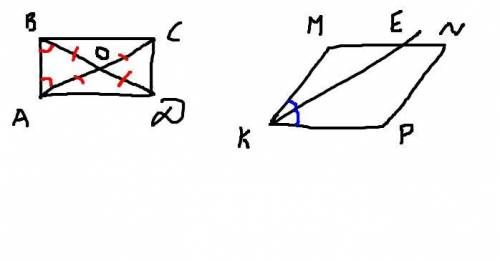
1. Диагонали прямоугольника пересекаются и точкой пересечения делятся на 4 равные части. Значит, AO = BO, и ΔAOB равнобедренный по определению ( с основанием AB). По свойству углов при основании равнобедрнного треугольника <ABO = <BAO = 30°.

Сумма углов треугольника 180°, поэтому

<AOB = 180° - <ABO - <BAO = 180° - 30° - 30° = 120° - угол между диагоналями.

2.а) Так как KE - биссектриса, то <MKE = <EKP

Так же <EKP = <MEK ( внутренние накрест лежащие углы при MN ║ KP и секущей KE)

Значит, <MKE = <EKP = <MEK, и ΔKME равнобедренный по признаку равнобедренного треугольника.

б) KM + MN = P(KMNP)/2 = 52/2 = 26 см

KM = ME = 10 см

KP = MN = 26 - KM = 26 - 10 = 16 см

Вариант 2

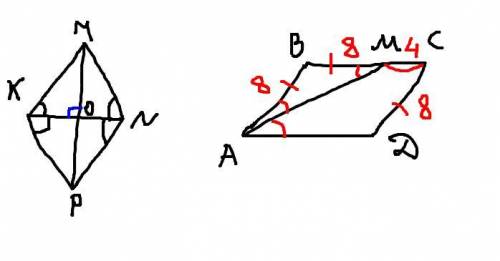
1. По свойству противоположных углов ромба <MKP = <MNP = 40°

Диагонали ромба являются биссектрисами его углов, значит, <MKO = <MKP/2 = 20°

Также диагонали параллелограмма перпендикулярны, поэтому <KOM = 90°.

Сумма углов треугольника 180°, поэтому

<KMO = 180° - <KOM - <MKO = 180° - 90° - 20° = 70°

Итого <KMO = 70°, <KOM = 90°, <MKO = 20°

2. а) AB = BM , значит ΔABM равнобедренный по определению, и по свойству углов при основании равнобедренного треугольника <BAM = <BMA.

<BMA = <MAD (внутренние накрест лежащие углы при BC ║ AD и секущей AM.

Следовательно, <BMA = < MAD, и AM - биссектриса <BAD.

б) AB = CD = 8 см (противоположные стороны параллелограмма равны)

BC = BM + CM

BM = AB (так как ΔABM равнобедренный)

BC = 8 + 4 = 12 см

P(ABCD) = 2*(AB+BC) = 2*(8 + 12) = 40 см

надя7488

Геометрия

4,8(35 оценок)

Тк треугольник равнобедренный, углы при основании равны. если угол, прилежащий к основанию, одного треугольника соответственно равен углу, прилежащему к основанию, другого, то оба угла при основании одного треугольника равны углам при основании другого, следовательно равнобедренные треугольники равны по стороне и прилежащим к ней углам (2 признак равенства треугольников)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.