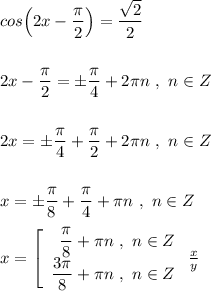Алгебра: Cos(2x-п/2)=√2/2 тригономическое уравнение решить

умникARM

24.05.2020 16:40

Алгебра

Есть ответ 👍

Cos(2x-п/2)=√2/2 тригономическое уравнение решить

166

433

Посмотреть ответы 3

Ответы на вопрос:

maximfz

Алгебра

4,6(3 оценок)

Уравнение

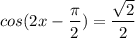
$cos(2x-\dfrac{\pi}{2}) = \dfrac{\sqrt2}{2}$

Для начала сделаем преобразование левой части уравнения: используем переместительный закон, чтобы изменить порядок членов, затем вынесем знак минуса за скобки, избавимся от минуса за счет свойств честности или нечетности тригонометрических функций, и, наконец используем выражение 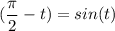$(\dfrac{\pi}{2} - t) = sin (t)$ для преобразования.

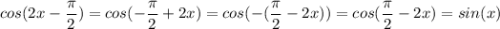
$cos(2x-\dfrac{\pi}{2}) = cos(-\dfrac{\pi}{2}+2x) = cos(-(\dfrac{\pi}{2}-2x)) = cos(\dfrac{\pi}{2}-2x) = sin(x)$

После преобразования решаем далее

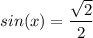
$sin(x) = \dfrac{\sqrt2}{2}$

Уравнение имеется два решения

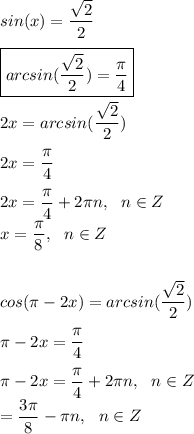
$sin(x) = \dfrac{\sqrt2}{2} \\\\ \boxed { arcsin(\dfrac{\sqrt2}{2})= \dfrac{\pi}{4}}\\\\2x = arcsin(\dfrac{\sqrt2}{2})\\\\2x = \dfrac{\pi}{4}\\\\2x = \dfrac{\pi}{4} + 2\pi n, ~~n \in Z\\x = \dfrac{\pi}{8}, ~~n \in Z \\\\\\cos(\pi - 2x) =arcsin(\dfrac{\sqrt2}{2})\\\\\pi-2x= \dfrac{\pi}{4}\\\\\pi -2x=\dfrac{\pi}{4}+2\pi n,~~n \in Z\\\x = \dfrac{3\pi}{8}-\pi n,~~n \in Z$

ответ

$\boxed{x= \begin{cases} \dfrac{\pi}{8}+\pi n, \\\\ \dfrac{3\pi}{8}+\pi n \end{cases},~~ n \in Z}$

Теразини

Алгебра

4,4(85 оценок)

$cos\Big(2x-\dfrac{\pi}{2}\Big)=\dfrac{\sqrt2}{2}\\\\\\2x-\dfrac{\pi}{2}=\pm \dfrac{\pi}{4}+2\pi n\ ,\ n\in Z\\\\\\2x=\pm \dfrac{\pi}{4}+\dfrac{\pi}{2}+2\pi n\ ,\ n\in Z\\\\\\x=\pm \dfrac{\pi}{8}+\dfrac{\pi}{4}+\pi n\ ,\ n\in Z\\\\x=\left[\begin{array}{l}\ \, \dfrac{\pi}{8}+\pi n\ ,\ n\in Z \\ \dfrac{3\pi}{8}+\pi n\ ,\ n\in Z\end{array}\right\frac{x}{y}$

srskimry

Алгебра

4,7(56 оценок)

(9-x^2)/(3x^2-2x-1)≥0,

(9-x^2)(3x^2-2x-1)≥0, 3x^2-2x-1≠0,

(9-x^2)(3x^2-2x-1)≥0,

9-x^2=0,

(3-x)(3+x)=0,

x1=-3,x2=3,

3x^2-2x-1=0,

d1=4,

x3=-1/3, x4=1,

-(x+3)(x+1/3)(x-1)(x-3)≥0,

(x+3)(x+1/3)(x-1)(x-3)≤0,

x∈[-3; -1/3)u(1; 3],

-3+(-2)+(-1)+2+3=-1

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.