Регистрация Спросить otvet5GPT
panda2438
07.06.2020 05:49
Алгебра
Есть ответ 👍

Исследовать знакопеременный ряд на абсолютную и условную сходимость

198
311
Посмотреть ответы 2

Ответы на вопрос:

111122223
111122223
4,5(80 оценок)

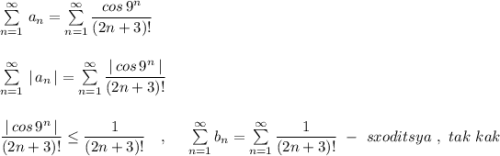
\sum \limits _{n=1}^{\infty }\, a_{n}=\sum \limits _{n=1}^{\infty }\dfrac{cos\, 9^{n}}{(2n+3)!}\\\\\\\sum \limits _{n=1}^{\infty }\, |\, a_{n}\, |=\sum \limits _{n=1}^{\infty }\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\\\\\\\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\leq \dfrac{1}{(2n+3)!}\ \ \ ,\ \ \ \ \sum \limits _{n=1}^{\infty }b_{n}=\sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}\ -\ sxoditsya\ ,\ tak\ kak

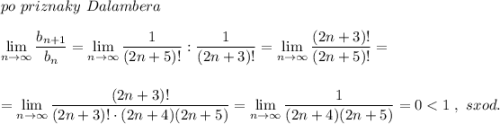
po\ priznaky\ Dalambera\\\\\lim\limits _{n \to \infty}\dfrac{b_{n+1}}{b_{n}}=\lim\limits _{n \to \infty}\dfrac{1}{(2n+5)!}:\dfrac{1}{(2n+3)!}=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+5)!}=\\\\\\=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+3)!\cdot (2n+4)(2n+5)} =\lim\limits _{n \to \infty}\dfrac{1}{(2n+4)(2n+5)}=0

Сходится мажорантный ряд 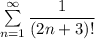  \sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}   , значит по признаку сравнения сходится и минорантный ряд  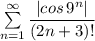   \sum \limits _{n=1}^{\infty }\dfrac{|cos\, 9^{n}|}{(2n+3)!}   -  ряд,

составленный из абсолютных величин исходного ряда.

Из сходимости ряда из абсолютных величин следует  абсолютная

сходимость исходного ряда .

муля15
муля15
4,8(9 оценок)

а)2200руб 

б)220

в)на 20 руб 3 год тоже на 20

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS