Геометрия: Нужно как то доказать, (простите за плохую фотку)

luizalol

12.01.2022 09:08

Геометрия

Есть ответ 👍

Нужно как то доказать,
(простите за плохую фотку)

151

334

Посмотреть ответы 3

Ответы на вопрос:

egyrt

Геометрия

4,7(2 оценок)

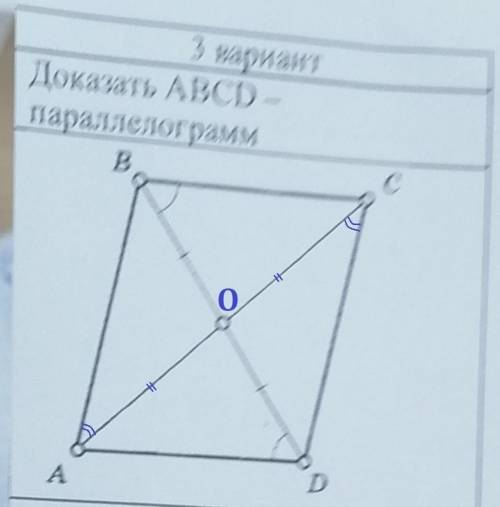
Параллелограмм - это четырехугольник, у которого противолежащие стороны попарно параллельны.

Если мы докажем, что BC║AD и AB║CD, то докажем, что ABCD параллелограмм.

1) ∠DBC = ∠BDA по условию, а это внутренние накрест лежащие углы при прямых BC и AD и секущей BD ⇒ BC║AD. (если внутренние накрест лежащие угли при двух прямых и секущей равны, то эти прямые параллельны).

2) ΔBOC = ΔAOD по второму признаку (стороне и двум углам):

BO = OD по условию, ∠OBC = ∠ODA по условию, ∠BOC = ∠AOD вертикальные углы.

В равных треугольниках соответствующие стороны равны. AO = OC

3) ΔAOB = ΔCOD по первому признаку:

BO = OD по условию, AO = OC по доказанному, ∠AOB = ∠COD - вертикальные углы.

Из равенства треугольников следует равенство соответствующих углов.

∠BAO = ∠DCO, это внутренние накрест лежащие углы при прямых AB и CD и секущей AC. ⇒ AB ║CD

4) В четырехугольнике ABCD AD║BC и AB ║ CD. Четырехугольник ABCD параллелограмм.

Доказано.

Нужно как то доказать, (простите за плохую фотку)

akbotawka02

Геометрия

4,8(9 оценок)

параллелограмм

Объяснение:

потому что диагонал-АС длиннее,чем диагонал-ВД

SharkKinger

Геометрия

4,6(34 оценок)

1) ∠о=90° , т.к. диагонали ромба пересекаются под прямым углом. если ав=вд и ав=ад, то δавд - равносторонний, и ∠в=60°. соответственно ∠а=30° 2) если в ромбе ∠в=120°, то значит δавд опять же получится равносторонним, т.е.сторона ромба равна меньшей диагонали, т.е. 5 см, а периметр р=20 см. и как "лучший ответ" не забудь отметить, ; )

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.