Найти точки экстремума функции (x^3 + 27) / (3x - x^2) С подробным решением

175

478

Посмотреть ответы 3

Ответы на вопрос:

AnyRam

Математика

4,6(27 оценок)

Берем производную, приравниваем к нулю

Производная = 3х^2-6x-9=0

Решаем уравнение

Д=36+3*4*9=144

х12=(6+-12)/6= -1 и 3

При х=0, производная = -9 (отрицательная, т. е фенкция убывает в этой области) , т. е. точки

При х=-1, у=-3 - максимум

При х=3, у=-35 - минимум

igor331

Математика

4,4(49 оценок)

Пошаговое объяснение:

Посчитаем производную

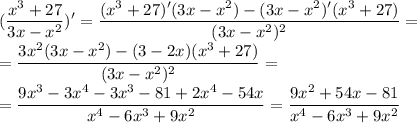
$\displaystyle (\frac{x^3 + 27}{3x - x^2})'=\frac{(x^3+27)'(3x-x^2)-(3x-x^2)'(x^3+27)}{(3x-x^2)^2} =\\= \frac{3x^2(3x-x^2)-(3-2x)(x^3+27)}{(3x-x^2)^2}=\\=\frac{9x^3-3x^4-3x^3-81+2x^4-54x}{x^4-6x^3+9x^2}=\frac{9x^2+54x-81}{x^4-6x^3+9x^2}$

Найдем её нули

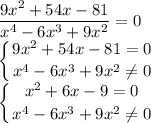
$\displaystyle\frac{9x^2+54x-81}{x^4-6x^3+9x^2}=0\\\left \{ {{9x^2+54x-81=0} \atop {x^4-6x^3+9x^2\neq 0}} \right. \\\left \{ {{x^2+6x-9=0} \atop {x^4-6x^3+9x^2\neq 0}} \right. \\$

Решим первое:

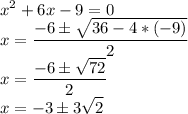
$\displaystyle x^2+6x-9=0\\x=\frac{-6\pm\sqrt{36-4*(-9)}}{2}\\x=\frac{-6\pm\sqrt{72}}{2}\\x=-3\pm3\sqrt2$

Ни один из этих корней не противоречит предыдущему условию. Значит мы нашли точки экстремума!

dimonm079

Математика

4,4(2 оценок)

У меня тоже этот сор отправтье

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.