Ответы на вопрос:
- 3,77m+9+5,3=(6+5,3)-3,97
-3,77m+14,3=11,3-3,97m
10,53m неравняется 7,33
ответ:не является тождеством
Объяснение:
Просто раскрывает скобки и сравниваем
−3,77m+9+5,3=(6+5,3)−3,97m
-3,77m + 14,3 = 11,3 - 3,97m
-3,77m + 3,97m = 11,3 - 14,3
0,2m = -3
m= -3:0,2
m = -15
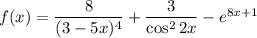
Совокупность всех первообразных функции 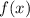 называют неопределенным интегралом:
называют неопределенным интегралом:
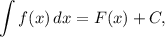
где 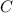 — произвольная постоянная.
— произвольная постоянная.
Тогда 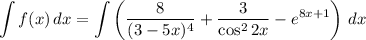
Теорема: если функции 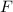 и
и 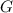 являются соответственно первообразными функций
являются соответственно первообразными функций 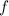 и
и 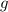 на промежутке
на промежутке 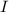 , то на этом промежутке функция
, то на этом промежутке функция 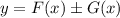 является первообразной функции
является первообразной функции 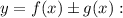
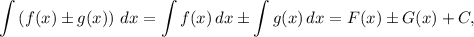
где 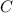 — произвольная постоянная.
— произвольная постоянная.
Тогда 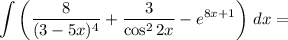
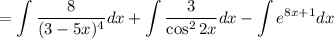
Теорема: если функция 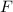 является первообразной для функции
является первообразной для функции 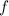 на промежутке
на промежутке 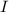 , а
, а 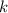 — некоторое число, то на этом промежутке функция
— некоторое число, то на этом промежутке функция 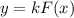 является первообразной функции
является первообразной функции 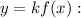
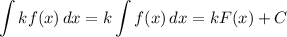
Тогда 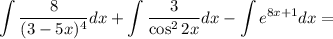
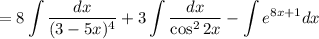
Теорема: если функция 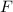 является первообразной для функции
является первообразной для функции 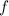 на промежутке
на промежутке 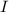 , а
, а 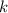 — некоторое число, отличное от нуля, то на соответствующем промежутке функция
— некоторое число, отличное от нуля, то на соответствующем промежутке функция 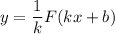 является первообразной функции
является первообразной функции 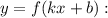
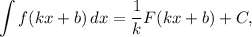
где 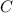 — произвольная постоянная.
— произвольная постоянная.
Найдем каждый интеграл по отдельности:
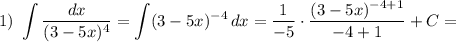
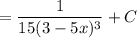
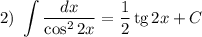
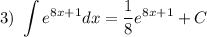
Получаем: 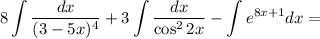
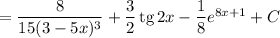
Таким образом, общий вид первообразных для функции 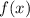 имеет вид:
имеет вид:
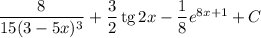
ответ: 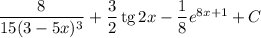
Использованные формулы интегрирования:
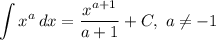
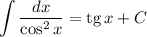
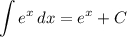
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Найдите координаты точки пересечения графика функций у=16х+32 с осью абсцисс....
 palechov0130.09.2020 17:17
palechov0130.09.2020 17:17 -
Спростіть вираз (6x-y)(6x+y)+(x+3y)(3y-x) (фото)...
 kolika201614.02.2022 16:22
kolika201614.02.2022 16:22 -
Решить с подробным решением ...
 georgijandreev103.08.2020 13:55
georgijandreev103.08.2020 13:55 -
Плачу все тесты сделать. Заплачу...
 y4enik502.02.2020 15:44
y4enik502.02.2020 15:44 -
Pamagite хотя бы что-то решите...
 zdiana131.01.2022 14:43
zdiana131.01.2022 14:43 -
5. ( ) Caлу есебін берілген бурыштын биссетрисасын салыңыз...
 polsmilе27.10.2022 22:25
polsmilе27.10.2022 22:25 -
Освободите от иррациональности в знаменателе ...
 оалклклкл29.10.2021 06:14
оалклклкл29.10.2021 06:14 -
, решить!! Решите неравенство: а) sin x ≥ √3\2 б) cos x\3 ≥√2\2...
 данил208114.09.2021 20:03
данил208114.09.2021 20:03 -
Розв язком якого рівняння є пара чисел (1;3) А) 2х+у=6 Б) 2х-у=0 В) 2х+у=5 Г) 2х-у=1...
 pineapplenastya122.01.2020 16:47
pineapplenastya122.01.2020 16:47 -
Палатка имеет форму правильной четырёхугольной пирамиды, сторона основания которой...
 mbolzhatova06.10.2022 16:31
mbolzhatova06.10.2022 16:31

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
