Алгебра: Возведите в степень 3² 6² 5³ 8²

Из основного тригонометрического тождества , если разделить обе его части на , cледует другое тождество : . Им и надо пользоваться при решении этих примеров . ...

asyamursalova12

26.04.2020 12:12

Алгебра

Есть ответ 👍

Возведите в степень
3²
6²
5³
8²

111

242

Посмотреть ответы 3

Ответы на вопрос:

MadMax22277

Алгебра

4,4(11 оценок)

125

Объяснение:

Чтобы найти степень числа надо умножить само число на самого себя столько раз сколько указано,допустим 2²=2×2 6²=6×6 5³=5×5×5

lolo2005

Алгебра

4,5(73 оценок)

Объяснение:

3²=9 6²=36 5³=125 8²=64

milk890098

Алгебра

4,6(64 оценок)

Из основного тригонометрического тождества 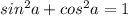sin^2a+cos^2a=1 , если разделить обе его части на 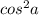cos^2a , cледует другое тождество :

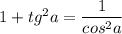$1+tg^2a=\dfrac{1}{cos^2a}$ . Им и надо пользоваться при решении этих примеров .

$2)\ \ tg\beta =-2dfrac{sin\beta \, cos\beta -3}{6\, cos^2\beta -sin^2\beta }=\dfrac{cos^2\beta \cdot \Big(\dfrac{sin\beta }{cos\beta }-3\cdot \dfrac{1}{cos^2\beta }\Big)}{cos^2\beta \cdot \Big(6-\dfrac{sin^2\beta }{cos^2\beta }\Big)}=\dfrac{tg\beta -3\cdot (1+tg^2\beta )}{6-tg^2\beta }==\dfrac{tg\beta -3-3\, tg^2\beta }{6-tg^2\beta }=\dfrac{-2-3-3\cdot 4}{6-4}=\dfrac{-5-12}{2}=\dfrac{-17}{2}=-8,5$

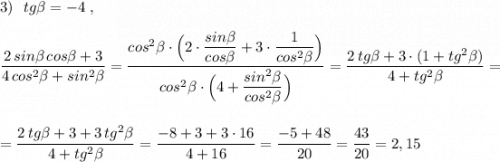
$3)\ \ tg\beta =-4\ ,dfrac{2\, sin\beta \, cos\beta +3}{4\, cos^2\beta +sin^2\beta }=\dfrac{cos^2\beta \cdot \Big(2\cdot \dfrac{sin\beta }{cos\beta }+3\cdot \dfrac{1}{cos^2\beta }\Big)}{cos^2\beta \cdot \Big(4+\dfrac{sin^2\beta }{cos^2\beta }\Big)}=\dfrac{2\, tg\beta +3\cdot (1+tg^2\beta )}{4+tg^2\beta }==\dfrac{2\, tg\beta +3+3\, tg^2\beta }{4+tg^2\beta }=\dfrac{-8+3+3\cdot 16}{4+16}=\dfrac{-5+48}{20}=\dfrac{43}{20}=2,15$

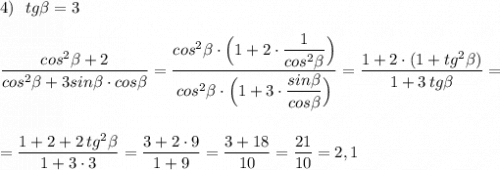
$4)\ \ tg\beta =3dfrac{cos^2\beta +2}{cos^2\beta +3sin\beta \cdot cos\beta }=\dfrac{cos^2\beta \cdot \Big(1+2\cdot \dfrac{1}{cos^2\beta }\Big)}{cos^2\beta \cdot \Big(1+3\cdot \dfrac{sin\beta }{cos\beta }\Big)}=\dfrac{1+2\cdot (1+tg^2\beta )}{1+3\, tg\beta }==\dfrac{1+2+2\, tg^2\beta }{1+3\cdot 3}=\dfrac{3+2\cdot 9}{1+9}=\dfrac{3+18}{10}=\dfrac{21}{10}=2,1$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Mdsk01
10.07.2020 04:28

при каких значениях a точка b(2;a) проходят через точку...
kremerartem1
13.03.2020 20:45

F(x;y)=arcsin(x+y) найти df/dx (1;-1/2)...
Bastricov
16.06.2021 09:50

При каком значении параметра корнем уравнения −х +2а −9 = 6 является число...
aziret31101
08.02.2023 16:24

414, Представьте в виде степени частное: а) х : х. в) ал: a; б) у : y ;...
MatveiKnyaz2005
12.03.2021 06:39

Найдите первый член и знаменатель геометрической прогрессии, если b_{4}...
zekisroman
11.01.2021 07:49

Решите неравенство log от 0.5(x^2-5x+6) -1...
leralerav
07.01.2021 12:14

Разложить на множетели 2ху-6х в 2, вынесением общего множетеля за скобки...
Eгор43
17.04.2020 21:23

Y=x(x+1)(x-1) исследовать и построить график данной функции....
ывывывывыв
08.06.2022 01:45

Люди добрые 1)36^{0.5-log_{6} \sqrt{5} } 2)log_{2} 4 \sqrt{8} 3) \frac{2lg6-lg3}{lg144}...
Moontrick
14.08.2021 13:26

Разложить на множители x^2-4xy+4y^2-1 по формуле сокращенного умножение...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.