Высшая математика от
решить векторную задачу 5.4(нет не 1;25.) (Углы же даны не просто так наверное, и вектор и скаляр не одно и тоже)

104

294

Посмотреть ответы 2

Ответы на вопрос:

АлираПендрагон

Математика

4,8(65 оценок)

Пошаговое объяснение:

Запишем формулу скалярного произведения векторов:

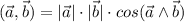
$(\vec{a},\vec{b})=|\vec{a}|\cdot |\vec{b}| \cdot cos(\vec{a} \land \vec{b})$

Т. к. скалярное произведение - линейное операция, то можем воспользоваться дистрибутивным и ассоциативным свойствами и преобразовать исходную запись:

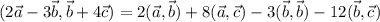
$(2\vec{a}-3\vec{b},\vec{b}+4\vec{c})=2(\vec{a},\vec{b})+8(\vec{a},\vec{c})-3(\vec{b},\vec{b})-12(\vec{b},\vec{c})$

Найдем все нужные скалярные произведения и подставим в полученное выше выражение:

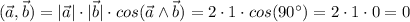
$(\vec{a},\vec{b})=|\vec{a}|\cdot |\vec{b}| \cdot cos(\vec{a} \land \vec{b})=2\cdot 1 \cdot cos(90^{\circ})=2\cdot 1 \cdot 0=0\\$

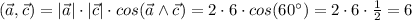
$(\vec{a},\vec{c})=|\vec{a}|\cdot |\vec{c}| \cdot cos(\vec{a} \land \vec{c})=2\cdot 6 \cdot cos(60^{\circ})=2\cdot 6 \cdot \frac{1}{2}=6 \\$

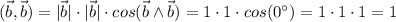
$(\vec{b},\vec{b})=|\vec{b}|\cdot |\vec{b}| \cdot cos(\vec{b} \land \vec{b})=1\cdot 1 \cdot cos(0^{\circ})=1\cdot 1 \cdot 1=1\\$

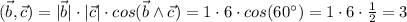
$(\vec{b},\vec{c})=|\vec{b}|\cdot |\vec{c}| \cdot cos(\vec{b} \land \vec{c})=1\cdot 6 \cdot cos(60^{\circ})=1\cdot 6 \cdot \frac{1}{2}=3$

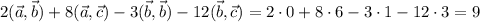
$2(\vec{a},\vec{b})+8(\vec{a},\vec{c})-3(\vec{b},\vec{b})-12(\vec{b},\vec{c})=2\cdot 0+8\cdot 6 -3\cdot 1 -12\cdot 3=9$

Alina2627848

Математика

4,4(52 оценок)

350*4+100=1400+100=1500м=1 км 500м вроде так, а лучше делать самой

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.