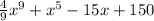Регистрация Спросить otvet5GPT
fenziknata
20.02.2020 02:21
Математика
Есть ответ 👍

Вычислите производную \frac{4}{9}x^9+x^5-15x+150

140
478
Посмотреть ответы 2

Ответы на вопрос:

yusifmailov1
yusifmailov1
4,4(90 оценок)

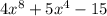
4x^{8} +5x^{4}-15

Пошаговое объяснение:

с'=0

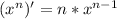
(x^n)' = n*x^{n-1}

x' = 1

вот формулы которые я использовал в этом примере.

muralova
muralova
4,4(91 оценок)
Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй — со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?

решение задач на встречное движение

Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:

1) 100 · 4 = 400 (км) — проехал первый автомобиль,

2) 70 · 4 = 280 (км) — проехал второй автомобиль.

Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:

400 + 280 = 680 (км).

Данную задачу можно решить и другим . Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч — это скорость сближения автомобилей. За 4 часа они проехали расстояние:

170 · 4 = 680 (км).

Таким образом, задачу на встречное движение можно решить двумя :

1-й : 2-й :
1) 100 · 4 = 400 (км) 1) 100 + 70 = 170 (км/ч)
2) 70 · 4 = 280 (км) 2) 170 · 4 = 680 (км)
3) 400 + 280 = 680 (км)
ответ: Населённые пункты находятся на расстоянии 680 км.

burgerking.ru
реклама
Перейти на сайт

Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?

как решать задачи на встречное движение

Решение: Сначала можно определить сколько километров каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:

1) 4 · 5 = 20 (км первый пешеход,

2) 5 · 5 = 25 (км второй пешеход.

Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:

20 + 25 = 45 (км).

Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:

70 - 45 = 25 (км).

У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:

4 + 5 = 9 (км/ч).

Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):

9 · 5 = 45 (км).

А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:

70 - 45 = 25 (км).

Таким образом, данная задача имеет два варианта решения:

1-й : 2-й :
1) 4 · 5 = 20 (км) 1) 4 + 5 = 9 (км/ч)
2) 5 · 5 = 25 (км) 2) 9 · 5 = 45 (км)
3) 20 + 25 = 45 (км) 3) 70 - 45 = 25 (км)
4) 70 - 45 = 25 (км)
ответ: Через 5 часов расстояние между пешеходами будет 25 км.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS