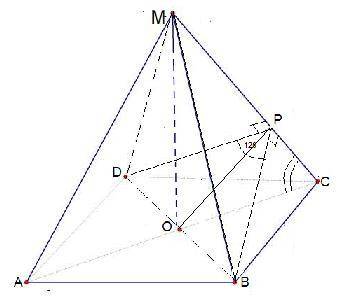
Двугранный угол при боковом ребре правильной четырехугольной пирамиды 120°. Нати угол между ребром и основанием
Ответы на вопрос:
Двугранный угол при боковом ребре правильной четырехугольной пирамиды 120°. Найти угол между ребром и основанием
Объяснение:
1) Пусть ВР⊥МС. Соединим Р и D.
ΔВРС=ΔDРС по 2 сторонам и углу между ними :РС-общая, ВС=DC как стороны квадрата ,∠РСВ=∠РСD как углы равных треугольников боковых граней.. Поэтому DР⊥МС и ∠DРВ- линейный угол двугранного угла при боковом ребре,∠DРВ=120°.
2) Углом между ребром МС и основанием АВСD будет угол между наклонной МС и ее проекцией СО⇒ ∠РСО.
РО∈(ВРD) ⇒РО⊥МС , значит ΔОРС-прямоугольный , sin(∠РСО)= 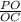 .
.
3) Пусть РВ=РD=х , для ΔBDP применим т. косинусов
BD²=х²+х²-2х²cos120 ( cos120=0,5) , BD²=3x² , BD=x√3.
Значит , половина диагонали квадрата , ОС=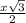 .
.
4) РО для ΔBDP является медианой, высотой биссектрисой. Поэтому ΔОРВ- прямоугольный, ∠ОРВ=60° →∠ОВР=30°⇒ катет РО=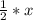 .
.
5) sin(∠РСО)= 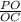 , sin(∠РСО)=
, sin(∠РСО)= 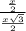 =
=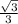 , ∠РСО=arcsin
, ∠РСО=arcsin 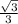 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
На рисунке ⦟T⦟P, TО PО. Докажите, что треугольник GОH– равнобедренный...
 dieric27.06.2022 00:59
dieric27.06.2022 00:59 -
Я просто по геометрии полный 0...
 Витаминка899007.05.2022 22:04
Витаминка899007.05.2022 22:04 -
Рисунок 1 . Диагонали прямоугольника ABCD пересекаются в точке 0. Най-...
 DarthRevan821.04.2021 18:29
DarthRevan821.04.2021 18:29 -
Периметр равнобедренной трапеции равен 60 см. Большее основание в 2...
 Alou1614.04.2023 00:14
Alou1614.04.2023 00:14 -
Что такое секс?Я не знаю...
 Evildevil221.03.2021 09:52
Evildevil221.03.2021 09:52 -
В прямоугольнике одна сторона в 3 раза больше другой, а площадь равна...
 Гиперборея29.09.2020 04:12
Гиперборея29.09.2020 04:12 -
Решить всё (с дано, и с чертежами) 100 ...
 janneellz02.10.2022 10:47
janneellz02.10.2022 10:47 -
Втреугольнике авс угол с равен 90 градусов. ав=50, вс=5 корень из 51....
 hhwjsbjweujskzks17.06.2023 17:20
hhwjsbjweujskzks17.06.2023 17:20 -
Дана окружность угол овс равен 34 градуса. нужно найти угол вас...
 meimanby14.07.2020 21:22
meimanby14.07.2020 21:22 -
Найдите углы треугольника mnp, если угол n: m: p=1: 3: 5...
 ingab298904.06.2020 05:34
ingab298904.06.2020 05:34

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
