Решите систему, используя метод сложения уравнений: а) {x² + y² = 17,
x²-y² = -15;
б) 5x²-y² + 6x = 11,
x² + y² = 25
261
323
Ответы на вопрос:
а) 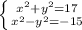
Сложим:

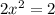
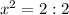
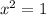
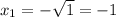
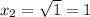
Подставим 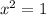 в первое уравнение:
в первое уравнение:
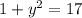
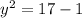
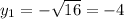
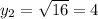
ответы: 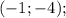
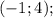
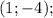
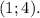
б) 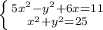
Сложим:
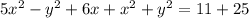
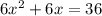
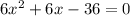
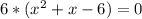
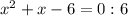
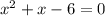
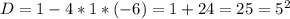
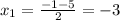
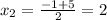
1) 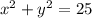 при
при 
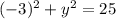
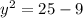
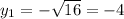
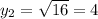
2) 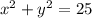 =>
=>  ₂ = 2
₂ = 2
2² + y² = 25
y² = 25 - 4
y² = 21
y₁ = - √21
y₂ = √21
ответы: 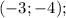
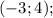
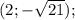
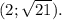
Пусть числа будут представлены в виде a и b. получим что: (a+b)/2 = 7, a^2-b^2=14. из среднего арифметического выразим a через b: (a+b)/2 = 7 a+b=14 а= 14-b подставим это значение а в разность квадратов и получим: (14-b)^2-b^2=14 196-28b+b^2-b^2=14 182=28b b=6.5 подставим значение b в формулу а= 14-b и найдем а = 7,5 тогда сумма квадратов: 7,5^2+6.5^2=56.25+42.25 = 98.5
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
(x² - 9)² + (x² -2x-15)²=0...
 1Kolomiets105.02.2020 03:00
1Kolomiets105.02.2020 03:00 -
Решить иррациональное уравнение: х в квадрате - 4х=3 корень из х в квадрате-4х+20-10...
 hitman1910200306.10.2022 06:12
hitman1910200306.10.2022 06:12 -
Постройте график функции y=-x+5...
 фейс407.07.2021 09:25
фейс407.07.2021 09:25 -
а5=0.5,а4=9.5 (аn)нужно найти арифметическую прогрессию...
 kair777555005.06.2020 15:07
kair777555005.06.2020 15:07 -
Дано: log25(7)=z. Вычисли: log7(625). log7(625)=...
 kzizh24.05.2023 17:34
kzizh24.05.2023 17:34 -
Қандай функцияны сызықтық функция деп атайды?...
 derver27.05.2021 07:52
derver27.05.2021 07:52 -
X(x+2) (x+3)(x-1) решить неравенство ...
 erka11211.11.2022 04:26
erka11211.11.2022 04:26 -
(1 курс) Решите оба примера(2.10) Для любого вещественного a доказать тождество:...
 zabzelilova13.09.2020 18:21
zabzelilova13.09.2020 18:21 -
Заполните пропуски При k не равном нулю нули функций y=f(x) и y=kf(x) . Графиком...
 penina104.03.2020 08:16
penina104.03.2020 08:16 -
Решите номер (549) пример (а) и (г)...
 angel2006200618.03.2023 18:18
angel2006200618.03.2023 18:18

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
