Регистрация Спросить otvet5GPT
diliana200405
06.07.2021 09:01
Математика
Есть ответ 👍

Докажите по индукции данное утверждение по подробнее

204
245
Посмотреть ответы 2

Ответы на вопрос:

alsusarip
alsusarip
4,8(49 оценок)

Условие не является полным. Это известное неравенство так называемое неравенство Бернулли и оно гласит, что для \alpha \geq -1 имеет место неравенство 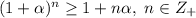(1+\alpha)^n\geq 1+n\alpha,~ n \in Z_+

1) При 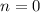n=0 база индукции выполнено: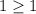 1\geq 1

2) Предположим, что для 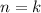n=k имеет место неравенство

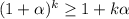
(1+\alpha)^k\geq 1+k\alpha

3) Докажем, что 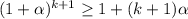(1+\alpha)^{k+1}\geq 1+(k+1)\alpha

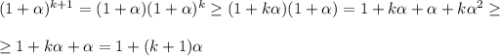
(1+\alpha)^{k+1}=(1+\alpha)(1+\alpha)^k\geq (1+k\alpha)(1+\alpha)= 1+k\alpha+\alpha+k\alpha^2\geq\\ \\ \geq1+k\alpha+\alpha=1+(k+1)\alpha

Неравенство верно из предположения 2). Утверждение доказано.

Полинаhelpme1
Полинаhelpme1
4,6(58 оценок)
1)25+45=70руб.- у миши 2)25+70=95руб.-у детей вместе 3)95+39=134руб-у родителей

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS