17.02.2021 14:21

Есть ответ 👍

Угол abc равен 45 градусов. на его стороне bc взята произвольная точка d и проведён de перпендикуляр ab.(e принадлежит ab) аналогично проведены ef перпендикуляр bc и fg перпендикулярна ab.(f принадлежит bc. а g принадлежит ab) найдите отрезок fg, если de=10см

158

164

Посмотреть ответы 2

Ответы на вопрос:

JeDor15

Геометрия

4,7(94 оценок)

Треугольник bef равнобедренный, т.к прямоугольный с углом в 45, его гипотенуза равна 10, а fg высота этого треугольника, а также его медиана. то есть bg=5, а треугольник bgf тоже равнобедренный и вg=gf=5

ГолубьФедя

Геометрия

4,7(28 оценок)

12 см

Объяснение:

Дано:

Сфера (O; R); R = 13

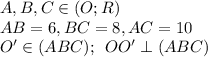
$A, B, C \in (O;R) \\ AB = 6, BC = 8, AC = 10 \\ \: O' \in (ABC); \: \: OO' \perp (ABC)$

Найти: ОО' - ?

Заметим, что

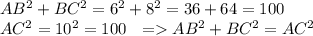
$AB^{2} + BC^{2} = {6}^{2} + {8}^{2} = 36 + 64 = 100 \\ \small AC^{2} = 10^{2} = 100 \: \: \: = AB^{2} + BC^{2} = AC^{2}$

=> ∆АВС - прямоугольный, с гипотенузой АС.

А следовательно, АС - это диаметр окружности, описанной вокруг ∆АВС; середина АС - центр такой окружности

Так как любая точка пространства, равноудалённая от точек А, В, С, не лежащих на одной прямой, принадлежит прямой, перпендикулярной плоскости (АВС); и прямая проходит через центр окружности, описанной около треугольника с вершинами в данных точках.

Соответственно, если ОО' _|_ (АВС) =>

=> О' - центр окружности, описанной вокруг ∆АВС =>

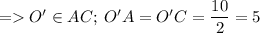
$= O' \in AC; \: O'A = O'C = \dfrac{10}{2} = 5$

Рассм. ∆АО'О:

ОО'_|_ (АВС) => ОО' _|_ АО' => уг.АО'О = 90°

=> ∆АО'О - прямоугольный, с гипотенузой АО = 13 см

По Т. Пифагора

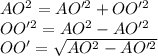
$AO^2 = AO'^2+OO'^2 \\ OO'^2= AO^2- AO'^2\\ \: OO'= \sqrt{AO^2- AO'^2}$

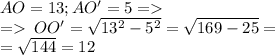
$AO = 13; AO' = 5 = \\ = \: OO' = \sqrt{13^2-5^2} = \sqrt{169 - 25} = \\ = \sqrt{144} = 12$

$OO' =12 \: cm$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.