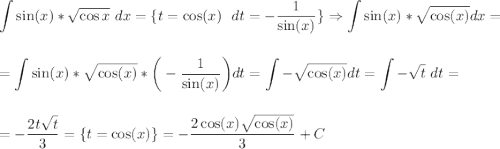Ответы на вопрос:
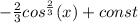
Объяснение:
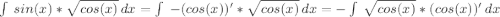
По формуле 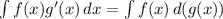
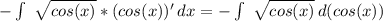
Пусть теперь 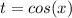 , тогда
, тогда
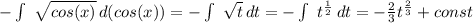
По формуле интеграла степенной функции: 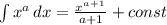
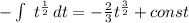
Учитывая нашу замену, запишем:
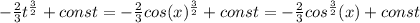
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Когда карантин щакончится в 5003 года ...
 kristinka7505.03.2023 04:11
kristinka7505.03.2023 04:11 -
решить 1 Вычислите 2 Выполните действия 3 Решить неравенство 4 Решить систему...
 faiarina201613.12.2020 02:29
faiarina201613.12.2020 02:29 -
Вычислите значение суммы первых пяти членов геометрической прогрессии, если:...
 yliuagulian20.10.2021 01:57
yliuagulian20.10.2021 01:57 -
У выражение 5 А + 2 Б - 15 а23 А Найдите значение этого выражения при а равно...
 sadpepeee14.02.2020 11:18
sadpepeee14.02.2020 11:18 -
10 корень из x + 7 корень из x-3 корень из q...
 mmmaaassshx03.09.2021 12:18
mmmaaassshx03.09.2021 12:18 -
Дана дробь, знаменатель которой на 12 больше числителя. если от числителя и...
 iVorobey15.01.2020 16:27
iVorobey15.01.2020 16:27 -
Разность 9 и четвёртого члена арифметической прогресии равна -90 а шестой член...
 theta4ka19.07.2021 19:33
theta4ka19.07.2021 19:33 -
Решите уравнение x2 ...
 mokovanins19.08.2020 03:19
mokovanins19.08.2020 03:19 -
УМОЛЯЮ ЗАЧЁТ 30 МИНУТ ОСТАЛОСЬ ХОТЯ БЫ 2 РЕШИТЕ...
 tryx329.04.2020 20:16
tryx329.04.2020 20:16 -
Найди чётное шестизначное натуральное число, сумма цифр которого равна их произведению....
 Аккерман1111.09.2022 12:25
Аккерман1111.09.2022 12:25

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.