Ответы на вопрос:
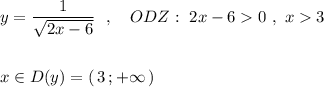
Функция всюду на ОДЗ принимает положительные значения: y>0 .
Точек пересечения с осями координат не имет .
Асимптоты: х=3 и у=0 .
На ОДЗ функция всюду убывает .
Точек экстремума и перегиба нет.
График на рисунке .
![класс! 1) [tex]y= 1:\sqrt{2x-6} Тут одз или что-то такое!](/tpl/images/3827/3951/d4af1.jpg)
ответ:
r 2+ 5-
2 x
−1 r
y2 =a
−5 r
рис. 5:
при a = −1 и a = −5 графики имеют 2 общие точки, при
остальных значениях a одну общую точку.
ответ: a ∈ (−5; −1).
1.12. (егэ) найдите число корней уравнения
6x2 + 2x3 − 18x + n = 0 в зависимости от параметра n.
решение.
перепишем уравнение в виде
y 6
2x3 + 6x2 − 18x = −n. r 54 y1
аналогично 1.11 построим на
одном чертеже графики функций
y2 = −n и схематичный график y2 =−n
y1 = 2x3 +6x2 −18x для этого найдем
производную: y1 = 6x2 +12x−18 и 0 1 -
критические точки x1 = −3 и x2 = 1. −3 −10 r x
исследуя знаки производной, нетруд-
но убедиться, что x1 = −3 точка
максимума, а x2 = 1 точка ми-
нимума, причем ymax (−3) = 54; рис. 6:
ymin (1) = −10. функция y1 возрастает на интервалах (−∞; −3)
и (1; +∞) и убывает на интервале (−3; 1).
из рис. 6 видно, что исходное уравнение имеет три корня при
−10 < −n < 54 или −54 < n < 10; два корня при n = −54 и
n = 10; один корень при n < −54 и n > 10.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Площадь прямоугольный спортивной площадки для игры с мячом(регби)6175м²...
 paperghost28.03.2023 05:08
paperghost28.03.2023 05:08 -
1-cos² альфа tg альфа дробь sin альфа нужно упростить выражение,с решением...
 katunina2004ox971p23.01.2023 12:10
katunina2004ox971p23.01.2023 12:10 -
Найдите сумму и произведение корней уравнения х²+9х-7=0...
 mullakaeva8528.07.2020 09:07
mullakaeva8528.07.2020 09:07 -
Графік якої функції проходять через точку (1;2)? а)у=0,5х-2 б)у=2х в)у=-3х+1...
 Zubu27.04.2022 08:54
Zubu27.04.2022 08:54 -
У трьох книжках 992 сторінки. У другій книжці на 16 сторінок менше, ніж...
 daramir0214.11.2020 20:09
daramir0214.11.2020 20:09 -
2. неравенство (х - а)(2х + 1)(х + b) 0 имеет решение ( -1/2; -1) ∪ (3;...
 lizakaraseva004.01.2021 12:29
lizakaraseva004.01.2021 12:29 -
ДАЮ 30б ОЧЕНЬ Знайти загальний розвьязок та 3 частиних розв язки для...
 РаминаГасымлы24.04.2020 23:38
РаминаГасымлы24.04.2020 23:38 -
Решить примеры 1.xy+1=xy 2.3xy+2=3x+2y 3.6-2y+6x-2xy=0...
 Даник177116.03.2021 01:42
Даник177116.03.2021 01:42 -
Найдите значение выражения 9 корень из 7 ×2 корень из 2 ×корень из 14...
 koshka2615.12.2022 13:06
koshka2615.12.2022 13:06 -
Представьте,если возможно,в виде квадрата двучлена: 3)16ad+b^2+64a^2 4)4x^2-12x+9...
 howl11113.04.2020 21:49
howl11113.04.2020 21:49

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
