Математика: Пусть x, y, z 0. Докажите неравенство (x+y+z)(1/x+1/y+1/z)≥9

KaterinYu31

23.03.2021 15:22

Математика

Есть ответ 👍

Пусть x, y, z > 0. Докажите неравенство
(x+y+z)(1/x+1/y+1/z)≥9

101

300

Посмотреть ответы 3

Ответы на вопрос:

deadpool2478

Математика

4,7(73 оценок)

Пошаговое объяснение:

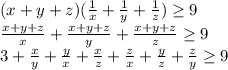
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})\geq 9\\\frac{x+y+z}{x}+\frac{x+y+z}{y}+\frac{x+y+z}{z}\geq 9\\3+\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}\geq 9$

Известно, что для положительных чисел a верно неравенство 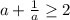$a+\frac{1}{a}\geq 2$ . Тогда

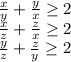
$\frac{x}{y}+\frac{y}{x}\geq 2\\\frac{x}{z}+\frac{z}{x}\geq 2\\\frac{y}{z}+\frac{z}{y}\geq 2$

Складывая эти неравенства получаем:

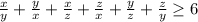
$\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}\geq 6$

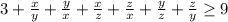
$3+\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}\geq 9$

Доказано.

Banannaa

Математика

4,5(92 оценок)

Используем неравенство между средним арифметическим и средним геометрическим для 3 положительных чисел а, в, с: (а+в+с)/3≥³√(авс) => (а+в+с)≥3*(³√(авс))

А тогда (x+y+z)(1/x+1/y+1/z)≥3(³√(xyz))(1/x+1/y+1/z)≥3(³√(xyz))*3(³√((1/x)(1/y)(1/z)))=9(³√(xyz))/(³√(xyz))=9*1=9

Ч.т.д.

(³√m) - кубический корень из числа m

stanislavgulya

Математика

4,5(95 оценок)

26Я не скпоровала потомучто

Пошаговое объяснение:

128+2=180 2=72 х=26

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.