Cледом квадратной матрицы называется сумма элементов её главной диагонали. Доказать, что для любых матриц A и B таких, что имеют
смысл оба произведения AB и BA, следы матриц AB и BA совпадают
119
339
Ответы на вопрос:
Пусть даны матрицы 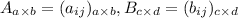 . Т.к. определено произведение
. Т.к. определено произведение 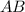 ,
, 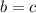 . Т.к. определено произведение
. Т.к. определено произведение 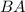 ,
, 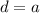 .
.
А значит даны матрицы 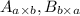
Пусть 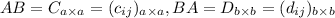 .
.
По определению, 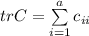 .
. 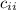 - сумма произведений соответствующих элементов iой строки матрицы A и iого столбца матрицы B, т.е.
- сумма произведений соответствующих элементов iой строки матрицы A и iого столбца матрицы B, т.е. 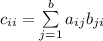 =>
=> 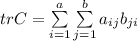
Аналогично 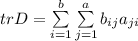
Т.к. пределы суммирования не зависят от переменных, то знаки суммирования можно поменять местами: 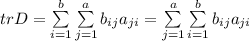
А теперь заметим, что, переобозначив переменные ![[i\to j;j\to i]](/tpl/images/3824/0204/a62a7.png) , получим
, получим 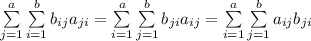 - а это и означает, что
- а это и означает, что 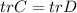
Ч.т.д.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Как решить уравнение x умножить на 19 = 285...
 lineage2920168226.05.2022 01:05
lineage2920168226.05.2022 01:05 -
Как найти площадь четырехугольника 3 класс...
 geroi2916.06.2022 11:43
geroi2916.06.2022 11:43 -
Сколько страниц в книге если было изпользованно 432 цифры...
 elyushik09.08.2020 08:13
elyushik09.08.2020 08:13 -
Прошу ! укажите пару взаимно простых чисел а)49 и 39 б)18 и 14. в)26 и 65....
 DarthTyranus24.12.2021 00:32
DarthTyranus24.12.2021 00:32 -
Используя цифры 2; 5 и 9(цифры не могут повторяться), запишите трехзначное...
 божена200610.03.2023 08:11
божена200610.03.2023 08:11 -
Округли числа до: десятков сотен тысяч 1543 872 135461 25 15013 10500 382 15...
 kissssss7s818.01.2020 19:10
kissssss7s818.01.2020 19:10 -
Улитку на бази видпочинку видпочивало 800 дитей у червни 250 дитей в липни...
 БеняФазбер01.10.2021 10:40
БеняФазбер01.10.2021 10:40 -
Нарисуй прямую и отметь 3 точки не на ней и 4 на ней...
 арина25654519.03.2020 05:51
арина25654519.03.2020 05:51 -
Реши уравнения с комментированием (х - 15)*40+80=320...
 артлжьт19.12.2020 05:27
артлжьт19.12.2020 05:27 -
Найти рациональным способом значение выражения 2/3(1,2+1,7+2,1+2,9+3,3+3,8)...
 Adalet55525.05.2020 08:14
Adalet55525.05.2020 08:14

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
