Ответы на вопрос:
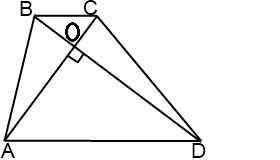
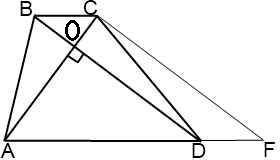
Дано: Трапеция ABCD;AC, BD - диагонали;∠AОD = 90°∠BDA = 60°Найти:Cреднюю линию трапеции - mРешение:1. Рассмотрим Треугольник АОD где ∠AОD = 90° (за условиям) и ∠BDA = 60° (тоже за условиям)за свойством треугольника сума всех углов равно 180°⇒ 180° = ∠AОD + ∠BDA + ∠ОАD⇒ ∠ОАD = 30° 2. Проведём высоту СN к остове AD( она будет перпендикулярна, ∠СNA=∠CND = 90°) Рассмотрим создавшейся треугольник ACN - прямоугольный (∠СNA = 90)Т. к. ∠ОАD = 30° то за свойством стороны которая лежит против угла 30° СN=1/2CA ⇒CN=5 cм3. "Диагонали трапеции перпендикулярны, решить задачу дополнительное построение."1) (Рис. сm2) Проведем через вершину меньшего основания прямую, параллельную диагонали: CF∥BD2) (Рис. сm3) Четырехугольник BCFD — параллелограмм, так как у него противоположные стороны лежат на параллельных прямых (CF∥BD по построению, BC∥AD как основания трапеции). Следовательно, DF=BC, CF=BD. Так как диагонали трапеции перпендикулярны, прямые CF и AC также перпендикулярны (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой). 4. Рассмотрим создавшейся треугольник СNF - прямоугольный ( ∠СNF = 90°)Т. к. ВD∥CF , а ВС∥DF и в следствии ВС∥AF⇒ ∠ВDF = ∠CFA = 60°Т. к. треугольник прямоугольный , тоsin∠CFN = 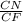 ⇒СF =
⇒СF = 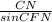 ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S =
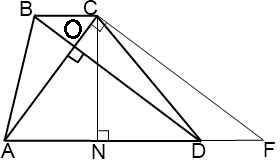
⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 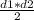 *sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m =
*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m = 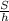 m =
m = 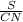 m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
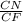 ⇒СF =
⇒СF = 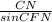 ⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S =
⇒ CF = 5/sin∠60°CF = 5/(√3/2)CF = 10/√3 cмCF = BD (cм пункт №3)⇒ BD = 10/√3 cм5. Рассмотрим трапецию ABCDЗа формулой S = 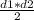 *sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m =
*sina где а = угол между диагоналями d1 и d2За условием диагонали перпендикулярны⇒ S =(BD*AC/2)* sin∠90°S =10*(10/√3)/2S =50/√3 cм²Так же площадь можно найти через среднюю линию и высоту за формулой:S = m · h⇒m = 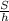 m =
m = 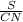 m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго...
m= (50/√3)/5m= 10/√3 cмответ: m= 10/√3 cмхух это было оч. долго... 


Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Продолжите последовательность (с объяснением): 2, 3, 3,...
 богдан25429.01.2023 22:36
богдан25429.01.2023 22:36 -
Найдите значение числового выражения 10-334•213+125: 159...
 karkavina8509.10.2021 02:32
karkavina8509.10.2021 02:32 -
Как записывается умножение,деление,сложение и вычитание десятичных дробей?...
 petrachenkov20106.06.2020 07:32
petrachenkov20106.06.2020 07:32 -
Решить примеры 99+501: 30*5-23= 72: 8+81: 30+17= 3*50-20: 13+90= 99+101: 20*6-15=...
 IMAM05778808.02.2020 09:54
IMAM05778808.02.2020 09:54 -
Найдите хнаяение выражения (4,3x-2,1x): 5,5 если x=4,1; x=2,3....
 alinab34605.12.2020 15:35
alinab34605.12.2020 15:35 -
Увадима а открыток.их в 2 раза меньше чем у алёши. сколько открыток у алёши...
 Nihilagay25.12.2020 22:32
Nihilagay25.12.2020 22:32 -
Учительниц на доске пишет числа в таком порядке: 5,10,15,20 какие следующие...
 сарвиназ00201.08.2022 04:16
сарвиназ00201.08.2022 04:16 -
Вычеслите первые 10 степеней числа 3...
 Варя100100503.10.2022 10:18
Варя100100503.10.2022 10:18 -
A*118=30122-2806 решить уравнение подробно...
 katyademona0412.05.2020 09:40
katyademona0412.05.2020 09:40 -
Подбери два числа,разность которых. равно 6 .назови несколько пар таких чисел...
 КамиляУшурова10.05.2022 15:10
КамиляУшурова10.05.2022 15:10

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
