Регистрация Спросить otvet5GPT
ЯНА1234598765
18.01.2021 04:08
Математика
Есть ответ 👍

Найти периметр квадрата со стороной 5м​

299
338
Посмотреть ответы 2

Ответы на вопрос:

Dodod616
Dodod616
4,6(9 оценок)

Пошаговое объяснение:

Чтобы найти периметр квадрата нужно его сторону умножить на 4. 5*4=20

ника3931
ника3931
4,4(10 оценок)

см. рисунок

Пошаговое объяснение:

Выполним понижение степени для синуса и косинуса в четвёртых степенях:

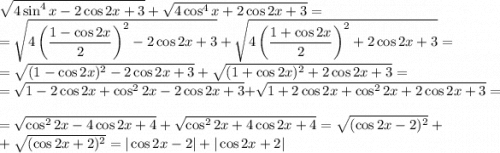
\sqrt{4\sin^4{x}-2\cos{2x}+3}+\sqrt{4\cos^4{x}+2\cos{2x}+3}=\\=\sqrt{4\left(\dfrac{1-\cos{2x}}{2}\right)^2-2\cos{2x}+3}+\sqrt{4\left(\dfrac{1+\cos{2x}}{2}\right)^2+2\cos{2x}+3}=\\=\sqrt{(1-\cos{2x})^2-2\cos{2x}+3}+\sqrt{(1+\cos{2x})^2+2\cos{2x}+3}=\\=\sqrt{1-2\cos{2x}+\cos^2{2x}-2\cos{2x}+3}+\sqrt{1+2\cos{2x}+\cos^2{2x}+2\cos{2x}+3}=\\=\sqrt{\cos^2{2x}-4\cos{2x}+4}+\sqrt{\cos^2{2x}+4\cos{2x}+4}=\sqrt{(\cos{2x}-2)^2}+\\+\sqrt{(\cos{2x}+2)^2}=|\cos{2x}-2|+|\cos{2x}+2|

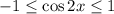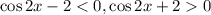Поскольку -1\leq \cos{2x}\leq 1, то \cos{2x}-2 < 0,\cos{2x}+2 0, и модули раскрываются однозначно:

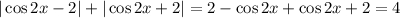
|\cos{2x}-2|+|\cos{2x}+2|=2-\cos{2x}+\cos{2x}+2=4

Тогда получаем функцию 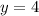y=4. Поскольку все преобразования были равносильны, область определения не меняется. В полученной функции это вся числовая прямая, значит, область определения исходной функции — тоже вся числовая прямая. График функции — см. ниже (зелёная линия).


Построить график функции

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS