Регистрация Спросить otvet5GPT
BellaNow
31.05.2023 22:24
Алгебра
Есть ответ 👍

решить уравнение arccos(x)=arctg(x/sqrt(1-x2))

156
359
Посмотреть ответы 2

Ответы на вопрос:

Дарья290705
Дарья290705
4,5(88 оценок)

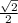
\frac{\sqrt{2}}{2}

Объяснение:

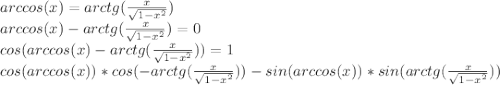
arccos(x) = arctg(\frac{x}{\sqrt{1 - x^2}} )\\arccos(x) - arctg(\frac{x}{\sqrt{1 - x^2}} ) = 0\\cos(arccos(x) - arctg(\frac{x}{\sqrt{1 - x^2}} )) = 1\\cos(arccos(x))*cos(-arctg(\frac{x}{\sqrt{1 - x^2}}))-sin(arccos(x))*sin(arctg(\frac{x}{\sqrt{1 - x^2}}))\\

Далее мы получаем, что

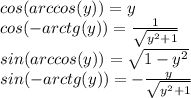
cos(arccos(y)) = y\\cos(-arctg(y)) = \frac{1}{\sqrt{y^2+1}} \\sin(arccos(y)) = \sqrt{1-y^2}\\sin(-arctg(y))=-\frac{y}{\sqrt{y^2+1} }

все это следует из основного тригонометрического тождества

Заменяем все по формулам:

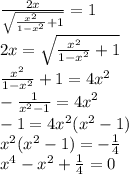
\frac{2x}{\sqrt{\frac{x^2}{1-x^2} +1} } =1\\2x=\sqrt{\frac{x^2}{1-x^2} +1} \\\frac{x^2}{1-x^2} +1=4x^2\\-\frac{1}{x^2-1} =4x^2\\-1=4x^2(x^2-1)\\x^2(x^2-1)=-\frac{1}{4} \\x^4-x^2+\frac{1}{4} =0

Заменим квадрат х на у и решим квадратное уравнение

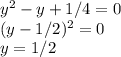
y^2-y+1/4=0\\(y-1/2)^2=0\\y=1/2

Вспомним, что 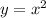y = x^2

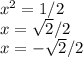
x^2=1/2\\x=\sqrt{2} /2\\x=-\sqrt{2} /2

проверим корни -

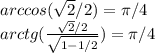
arccos(\sqrt{2}/2)=\pi/4\\arctg(\frac{\sqrt{2}/2}{\sqrt{1-1/2}})=\pi/4\\

положительный корень подходит.

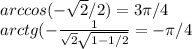
arccos(-\sqrt{2}/2)=3\pi/4\\arctg(-\frac{1}{\sqrt{2}\sqrt{1-1/2}} =-\pi/4

отрицательный не подходит.

отсюда ответ - 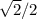\sqrt{2}/2

tamtamtamira
tamtamtamira
4,7(77 оценок)
(u - 2)(7u + 1)(3u - 7) = \\ = (u - 2)(21 {u}^{2} - 49u + 3u - 7) = \\ = (u - 2)(21 {u}^{2} - 46u - 7) = \\ = 21 {u}^{3} - 46 {u}^{2} - 7u - 42 {u}^{2} + 92u + 14 = \\ = 21 {u}^{3} - 88 {u}^{2} + 85u + 14

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS