Регистрация Спросить otvet5GPT
соня1583
05.07.2021 03:38
Алгебра
Есть ответ 👍

Знайти кількість натуральних двоцифрових чисел які при діленні на 3 дають в остачі 2​

251
483
Посмотреть ответы 2

Ответы на вопрос:

СуРиКан200606
СуРиКан200606
4,5(96 оценок)

30

Объяснение:

Натуральні числа, які при діленні на 3 дають в остачі 2​ мають загальний вигляд 3k+2, де k>=0, k є Z

Так як різниця між двома сусідніми числами (3(k+1)+2)-(3k+2)=2k+3+2-3k-2=3 - стала, то числа задають арифметичну прогресію з різницею d=2;.

Знайдемо перший член послідовності:

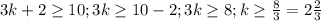
3k+2 \geq 10;3k \geq 10-2; 3k \geq 8;k \geq \frac{8}{3}=2\frac{2}{3}

=> k=3 - як найменше ціле число, що задовільняє нерівність

а саме число 3*3+2=9+2=11

Знайдемо останній член послідовності:

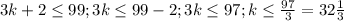
3k+2 \leq 99;3k \leq 99-2;3k \leq 97;k \leq \frac{97}{3}=32\frac{1}{3}

=> k=32 як найбільше ціле число, що задовільняє нерівність

а саме число 3*32+2=96+2=98

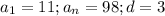
a_1=11;a_n=98;d=3

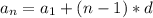
a_n=a_1+(n-1)*d

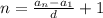
n=\frac{a_n-a_1}{d}+1

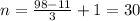
n=\frac{98-11}{3}+1=30


Знайти кількість натуральних двоцифрових чисел які при діленні на 3 дають в остачі 2​
Tjfjfjcgjgk
Tjfjfjcgjgk
4,5(88 оценок)
1) пусть е - сколь угодно большое положительное число. нужно доказать, что найдётся такое n=n, что при n> n будет n/3+1> e. решая неравенство n/3+1> e, находим n/3> e-1, откуда n> 3*(e+1).   но так как n⇒∞, то такое значение n=n всегда (то есть при любом е) найдётся. тем более это неравенство будет справедливо для всех ещё больших значений   n> n. а это и значит, что lim(n/3+1)=∞. 2) пусть е - сколь угодно большое по модулю отрицательное число. нужно доказать, что найдётся такое n=n, что при n> n будет 1-n²< e. это неравенство равносильно неравенству n²> 1-e, или n> √(1-e). так как 1-e> 0 и n⇒∞, то такое значение n=n   всегда найдётся. тем более это неравенство справедливо для всех ещё больших значений n> n. а это и значит, что lim(1-n²)=-∞.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS