Регистрация Спросить otvet5GPT
XxXRePlayXxX
07.01.2022 17:24
Алгебра
Есть ответ 👍

Докажите, что многочлен, тождественно равный выражению (x - 4)^2n + (x - 3)^n - 1, где n является натуральным, делится нацело га многочлен x^2 - 7x + 12

269
339
Посмотреть ответы 2

Ответы на вопрос:

rita239
rita239
4,7(96 оценок)

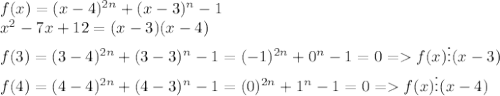
f(x)=(x - 4)^{2n} + (x - 3)^n - 1\\ x^2 - 7x + 12=(x-3)(x-4)\\ f(3)=(3 - 4)^{2n} + (3 - 3)^n - 1=(-1)^{2n} + 0^n - 1=0=f(x)\vdots (x-3)\\ f(4)=(4 - 4)^{2n} + (4 - 3)^n - 1=(0)^{2n} + 1^n - 1=0=f(x)\vdots (x-4)

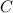(x-3) и (x-4) неприводимы над C (их степень равна 1) . А значит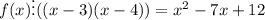 f(x)\vdots((x-3)(x-4))=x^2 - 7x + 12

Ч.т.д.

_____________________

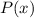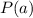В решении использована Теорема Безу: остаток от деления многочлена {\displaystyle P(x)} на двучлен {\displaystyle (x-a)} равен {\displaystyle P(a)}.

vtkmlth
vtkmlth
4,7(91 оценок)

ответ:

1)-1

объяснение:

номер 1.

6х-8у; х=2/3,у=5/8

6 умножить на 2/3=4

8у умножить на 5/8=5

4-5=-1

номер 2.

a)5a-3b-8a+12b=9b-3a=3(3b-a)

б)16c+(3c-2)-(5c+7)=16c+3c-2-5c-7=14c-9

остальное делай сам.

сколько врешь — столько и получаешь

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS