Математика: Соедините векторы с их суммой очень

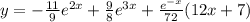
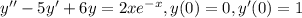
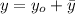
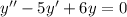
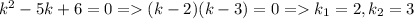
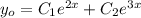
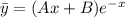
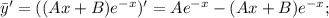
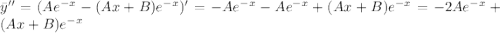
Пошаговое объяснение:Имеем дело с неоднородным линейным уравнением. 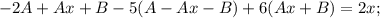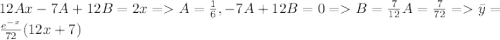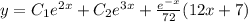Его решение можно искать в виде суммы общего решения однородного уравнения и частного решения неоднородного: Однородное уравнение: Его характеристическое уравнение: Общее решение однородного уравнения запишется в виде:Частное решение неоднородного уравнения имеет смысл искать в виде: Посчитаем производные:Подставляем в уравнение и сокращаем на экспоненту:Тогда общее решение запишется в виде:Определим константы из начальных условий:...

nikitka1011

03.03.2021 06:38

Математика

Есть ответ 👍

Соедините векторы с их суммой
очень

246

425

Посмотреть ответы 2

Ответы на вопрос:

puh9999

Математика

4,8(14 оценок)

1-2

2-1

3-4

4-3

Пошаговое объяснение:

katyabicheva

Математика

4,4(85 оценок)

$y = -\frac{11}{9}e^{2x} + \frac{9}{8}e^{3x}+\frac{e^{-x}}{72}(12x+7)$

Пошаговое объяснение:

$y''-5y'+6y=2xe^{-x}, y(0)=0, y'(0)=1$

Имеем дело с неоднородным линейным уравнением. Его решение можно искать в виде суммы общего решения однородного уравнения и частного решения неоднородного: $y=y_o+\bar y$

Однородное уравнение: y''-5y'+6y=0

Его характеристическое уравнение: k^2-5k+6 = 0 = (k-2)(k-3) = 0 = k_1=2,k_2=3

Общее решение однородного уравнения запишется в виде:

$y_o = C_1e^{2x}+C_2e^{3x}$

Частное решение неоднородного уравнения имеет смысл искать в виде: $\bar y = (Ax+B)e^{-x}$

Посчитаем производные:

$\bar y' = ((Ax+B)e^{-x})' = Ae^{-x}-(Ax+B)e^{-x};$

$\bar y'' = (Ae^{-x}-(Ax+B)e^{-x})' = -Ae^{-x} - Ae^{-x} + (Ax+B)e^{-x} = -2Ae^{-x}+(Ax+B)e^{-x}$

Подставляем в уравнение и сокращаем на экспоненту:

-2A+Ax+B -5(A-Ax-B)+6(Ax+B)=2x;

$12Ax -7A+12B = 2x = A=\frac{1}{6}, -7A+12B=0 = B=\frac{7}{12}A=\frac{7}{72} = \bar y = \frac{e^{-x}}{72}(12x+7)$

Тогда общее решение запишется в виде:

$y=C_1e^{2x}+C_2e^{3x} +\frac{e^{-x}}{72}(12x+7)$

Определим константы из начальных условий:

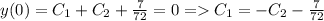
$y(0) = C_1+C_2+\frac{7}{72}=0 = C_1 = -C_2-\frac{7}{72}$

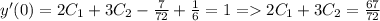
$y'(0) = 2C_1+3C_2-\frac{7}{72}+\frac{1}{6}=1 = 2C_1+3C_2 = \frac{67}{72}$

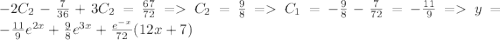
$-2C_2-\frac{7}{36}+3C_2=\frac{67}{72} = C_2 = \frac{9}{8} = C_1 = -\frac{9}{8}-\frac{7}{72} = -\frac{11}{9} = y = -\frac{11}{9}e^{2x} + \frac{9}{8}e^{3x}+\frac{e^{-x}}{72}(12x+7)$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.