решить! В равнобокой трапеции боковая сторона равна 6 см, а угол при основании равно 60 градусов, большее основание равно 24 см. Найти среднюю линию трапеции

241

257

Посмотреть ответы 2

Ответы на вопрос:

vasilchukanna1

Геометрия

4,6(20 оценок)

ответ: 21 см

( Среднюю линию нарисуйте сами на трапеции )

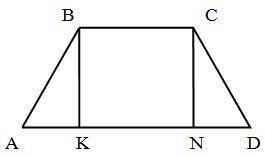
Дано :ABCD- трапеция, АВ=СD=6 см, ∠А=60° ,АD=24 см

Найти : среднюю линию трапеции.

Решение: Средняя линия трапеции - отрезок соединяющий середины боковых сторон(АВиСD) и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

Необходимо найти ВС, для этого из вершин В и С проведём высоты к основанию АD ( ВК ⊥АD и СN⊥АD ),

Рассмотрим ΔАВК, где АВ=6см, ∠А=60°, ∠К=90°, по теореме о сумме трёх углов треугольника ∠АВК= 180°-(90°+60°)=30°.

катет АК лежит против угла 30° прямоугольного треугольника АВК и равен половине гипотенузи АВ:

АК=60см:2=3 см.

Соответственно рассмотрев ΔСND , где ∠N=90°, ∠D=60°( как угол при основании равнобедренной трапеции) ∠DСN= 180°-(90°+60°)=30°.

ND =6см:2=3см( как катет , лежащий против угла 30° прямоугольного треугольника СND).

так как ВС║АD( как основания трапеции) ,ВК║СN( как перпендикуляры одной прямой) и ∠К=∠N=90°, то КВСN- прямоугольник , где ВС= КN

КN= АD-АК-ND=24-3-3=18(см), ВС= 18 см

Найдём длину средней линии: L=(АD+ВС):2=(24+18):2=21(см)

решить! В равнобокой трапеции боковая сторона равна 6 см, а угол при основании равно 60 градусов, бо

usik6

Геометрия

4,6(62 оценок)

Т.к. трапеция авсд равнобедренная, то углы а и д равны. угол а=угол д=124: 2=62(градуса), в трапеции сумма углов, прилежащих к одной боковой стороне, равна 180(градусов). угол с=180-угол д=180-62=118(градусов) ответ: угол с=118 градусов

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.