Регистрация Спросить otvet5GPT
Nastjadd
30.06.2023 23:57
Алгебра
Есть ответ 👍

Если f(x)=4/x найти нужна

160
354
Посмотреть ответы 2

Ответы на вопрос:

bodiafan
bodiafan
4,8(54 оценок)

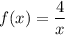
f(x)=\dfrac{4}{x}

При записи функции обычно переменную обозначают буквой "х" , функцию - буквой "у" .  

Но обозначать можно в принципе любыми буквами. Поэтому эту же функцию можно записать через переменную "t"  так: 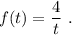 f(t)=\dfrac{4}{t}\ .  

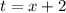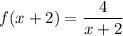А теперь легче сообразить , что если мы положим  t=x+2  ,  то функция    f(x+2)=\dfrac{4}{x+2} .

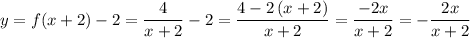
y=f(x+2)-2=\dfrac{4}{x+2}-2=\dfrac{4-2\, (x+2)}{x+2}=\dfrac{-2x}{x+2}=-\dfrac{2x}{x+2}

Tuchka087
Tuchka087
4,4(40 оценок)
Т.к. sin(x) - непрерывная функция, она интегрируема, и можно выбирать любое разбиение с любыми точками на нем. разобьем [a,b] на n равных частей и возьмем значения функции в левых точках получившихся отрезков: ∑ sin(a + k*(b-a)/n) * (b-a)/n, где k = 0 .. n-1 далее преобразуем слагаемые в разности косинусов: sin(a + k*(b-a)/n) = sin(a + k*(b-a)/n) * sin( (b-a)/2n ) / sin( (b-a)/2n ) = 1/(2sin((b-a)/2n)) * [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)] здесь были применены формулы cos(x+y) = cos(x)cos(y) - sin(x)sin(y) cos(x-y) = cos(x)cos(y) + sin(x)sin(y) тогда sin(x)sin(y) = 1/2 (cos(x-y) - cos(x+y)) где x = a + k*(b-a)/n, y = (b-a)/2n y было выбрано так, чтобы все косинусы, кроме крайних, попадали в сумму с разными знаками и сокращались. исходная сумма ∑ sin(a + k*(b-a)/n) * (b-a)/n преобразуется к виду (b-a)/n * 1/(2sin( (b-a)/2n )) * ∑ [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)], k = 0 .. n-1 т.к. cos(a + (k + 1/2) * (b-a)/n) = cos(a + ((k+1)-1/2) * (b-a)/n), соответствующие слагаемые в сумме сокращаются, как и рассчитывалось. т.е. ∑ [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)] = cos(a - 1/2 (b-a)/n) - cos(a + (n - 1/2)*(b-a)/n) при n ⇒ ∞, это выражение стремится к cos(a) - cos(b) что касается коэффициента (b-a)/n * 1/(2sin( (b-a)/2n )) перед суммой, при n ⇒ ∞ синус стремится к своему аргументу, т.е. (b-a)/n * 1/(2sin( (b-a)/2n )) ⇒ (b-a)/n * 1/(2 * (b-a)/2n)) = 1 т.е. сумма стремится cos(a) - cos(b) при n ⇒ ∞, причем этот предел по определению и является искомым определенным интегралом (диаметр разбиения (b-a)/n стремится к 0)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS