Регистрация Спросить otvet5GPT
PlatMasha
31.07.2021 17:23
Алгебра
Есть ответ 👍

Решить систему уравнений

124
475
Посмотреть ответы 2

Ответы на вопрос:

denisovavara11
denisovavara11
4,7(7 оценок)

Преобразуем первое уравнение системы:

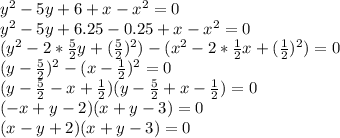
y^2-5y+6+x-x^2 = 0\\y^2 - 5y + 6.25 - 0.25 + x - x^2 = 0\\(y^2 - 2 * \frac{5}{2}y + (\frac{5}{2})^2) - (x^2 - 2*\frac{1}{2}x + (\frac{1}{2})^2)=0\\ (y-\frac{5}{2})^2 - (x-\frac{1}{2})^2=0\\ (y-\frac{5}{2}-x+\frac{1}{2})(y-\frac{5}{2}+x-\frac{1}{2})=0\\ (-x+y-2)(x+y-3)=0\\(x-y+2)(x+y-3)=0\\

Произведение равно нулю тогда, когда один из множителей равен нулю, а остальные существуют. Здесь ограничений на x и y нет, так что просто приравняем множители к нулю и рассмотрим два случая: первый, когда первый множитель ноль и второй, когда второй множитель ноль.

Первый случай:

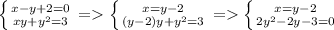
1) \left \{ {{x-y+2=0} \atop {xy+y^2=3}} \right. = \left \{ {{x = y - 2} \atop {(y-2)y+y^2=3}} \right. = \left \{ {{x=y-2} \atop {2y^2-2y-3=0}} \right.

Решаем второе уравнение системы:

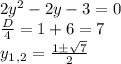
2y^2-2y-3=0\\\frac{D}{4} = 1 + 6 = 7\\ y_1_,_2 = \frac{1\pm\sqrt{7}}{2}

Теперь найдем соответствующие x:

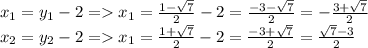
x_1 = y_1-2 = x_1 = \frac{1-\sqrt{7}}{2} - 2 = \frac{-3-\sqrt{7}}{2} = -\frac{3+\sqrt{7}}{2}\\x_2 = y_2 - 2 = x_1 = \frac{1+\sqrt{7}}{2}-2 = \frac{-3+\sqrt{7}}{2} = \frac{\sqrt{7}-3}{2}

Второй случай:

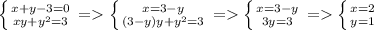
\left \{ {{x+y-3=0} \atop {xy+y^2=3}} \right. = \left \{ {{x = 3-y} \atop {(3-y)y+y^2=3}} \right. = \left \{ {{x=3-y} \atop {3y=3}} \right. = \left \{ {{x=2} \atop {y = 1}} \right.

Здесь вроде бы все понятно и без комментариев.

(-\frac{3+\sqrt{7}}{2}; \frac{1-\sqrt{7}}{2})\\ (\frac{\sqrt{7}-3}{2}; \frac{1+\sqrt{7}}{2})\\ (2;1)

bulkin12
bulkin12
4,6(1 оценок)
1) 2^-1 2^-3 2^-5 2) (1/3)^-4 (1/3)^-3 (1/3)^-2 (1/3)^0 (1/3)^1 (1/3)^2 (1/3)^3 (1/3)^4

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS