Найти все натуральные числа а и в такие что а^2 +b и b^2+a - квадраты

188

295

Посмотреть ответы 2

Ответы на вопрос:

катялисицина

Математика

4,5(16 оценок)

ответ: нет таких натуральных 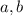a,b

Пошаговое объяснение:

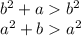
$b^2+ab^2\\a^2+ba^2$

Поскольку числа 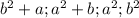b^2+a;a^2+b;a^2;b^2 полные квадраты, а числа 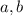a,b натуральные, то

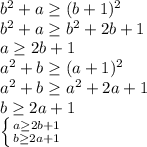
$b^2+a\geq (b+1)^2\\b^2+a\geq b^2+2b+1\\a\geq2b+1 \\a^2+b\geq(a+1)^2\\a^2+b\geq a^2+2a+1\\b\geq2a+1\\\left \{ {{a\geq 2b+1} \atop {b\geq 2a+1}} \right.$

Сложим полученные неравенства почленно:

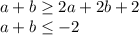
$a+b\geq 2a+2b+2\\a+b\leq -2$

Что невозможно для натуральных чисел и .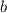

Как видим, таких натуральных и 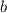не существует.

1Маша1231111

Математика

4,4(5 оценок)

25+25=50(тет)было в клетку и в линею. 50+18=68(тет) ответ: 28 тетрадей было у учителя.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.