Точка M — середина стороны BC параллелограмма ABCD. Выразите вектор AM через векторы AC и
BD.

155

248

Посмотреть ответы 2

Ответы на вопрос:

illay0409

Геометрия

4,4(32 оценок)

$\overrightarrow{AC} - \frac{1}{4} (\overrightarrow{AC} + \overrightarrow{BD})$

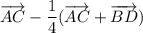
Объяснение:

Построим прямую CE параллельную DB.

DE - продолжение AD.

BCED - параллелограмм т.к. противолежащие стороны попарно параллельны. Следовательно DE = BC ; BD = CE.

Значит 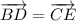$\overrightarrow{BD} = \overrightarrow{CE}$

$\overrightarrow{AC} + \overrightarrow{CE} = \overrightarrow{AE}$

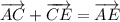
Пусть F - середина AD. Значит 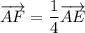$\overrightarrow{AF} = \frac{1}{4} \overrightarrow{AE}$

$\overrightarrow{AF} = \overrightarrow{MC}$

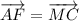
Собираем все вместе:

$\overrightarrow{MC} = \frac{1}{4} (\overrightarrow{AC} + \overrightarrow{BD})$

$\overrightarrow{CM} = - \overrightarrow{MC}$

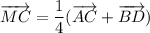
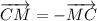
Т.к 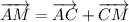$\overrightarrow{AM} = \overrightarrow{AC} + \overrightarrow{CM}$ , то $\overrightarrow{AM} = \overrightarrow{AC} - \frac{1}{4} (\overrightarrow{AC} + \overrightarrow{BD})$

============

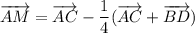
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Успехов в учебе

Точка M — середина стороны BC параллелограмма ABCD. Выразите вектор AM через векторы AC и BD.

tatulia32

Геометрия

4,7(95 оценок)

Впрямоугольном треугольнике гипотенуза равна двум радиусам описанной окружности ,а медиана,проведенная к гипотенузе равна радиусу описанной окружности.значчит медиана равна 16: 2=8см

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.