Регистрация Спросить otvet5GPT
керамбит1
30.12.2020 08:26
Алгебра
Есть ответ 👍

Два непропорциональных кубических многочлена с целыми коэффициентами имеют общий иррациональный корень. Докажите, что у них есть еще один общий корень

263
458
Посмотреть ответы 2

Ответы на вопрос:

vyachik2000
vyachik2000
4,8(37 оценок)

Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.

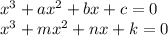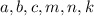x^3+ax^2+bx+c = 0\\x^3+mx^2+nx+k=0, a,b,c,m,n,k - рациональные числа.

Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:

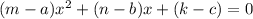(m-a)x^2+(n-b)x+(k-c) = 0 , поскольку коэффициенты уравнений непропорциональны, то все коэффициенты полученного квадратного уравнения ненулевые.

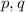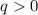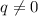А значит, данный общий иррациональный корень принимает вид : p+-\sqrt{q} , где p,q - рациональные числа, при этом q0 не полный квадрат, отсюда в частности q\neq 0.

Попробуем показать, что если 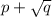 p+\sqrt{q} корень уравнения

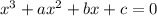x^3+ax^2+bx+c = 0 , то и 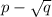p-\sqrt{q} корень данного уравнения , и наоборот. Сделаем некоторое упрощение.

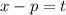Если число  p+-\sqrt{q}  является корнем данного уравнения , то сделаем замену:  x-p=t , тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень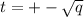  t=+-\sqrt{q}  

Такое уравнение примет вид :

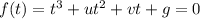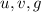f(t)=t^3+ut^2+vt+g=0 , u,v,g - рациональные числа.

Учитывая, что 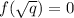f(\sqrt{q} ) = 0

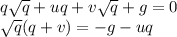
q\sqrt{q} +uq+v\sqrt{q} +g=0\\\sqrt{q} (q+v) = -g-uq

Предположим, что 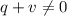q+v\neq 0 , но тогда , учитывая, что 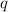q - не полный квадрат, то левая часть равенства иррациональна, а правая  рациональна, что невозможно. То есть мы пришли к противоречию, а значит :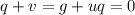 q+v=g+uq=0

Таким образом:

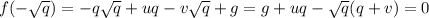
f(-\sqrt{q} ) =-q\sqrt{q} +uq -v\sqrt{q}+g = g+uq -\sqrt{q}(q+v) = 0

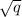Аналогично, доказывается, что если -\sqrt[]{q} корень данного уравнения, то и \sqrt{q} корень этого уравнения.

Таким образом, мы доказали, что если 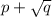 p+\sqrt{q} корень уравнения

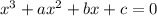x^3+ax^2+bx+c = 0 , то и 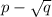p-\sqrt{q} корень данного уравнения и наоборот.  Аналогично доказывается этот факт и для уравнения:

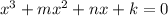x^3+mx^2+nx+k=0 .

А значит, данные кубические многочлены имеют еще один общий иррациональный корень.

Что и требовалось доказать.

СофаСофачка
СофаСофачка
4,8(94 оценок)
Р- вероятность, насколько я понял а) на кости выпало 6  б) на кости выпало 4 в) на кости выпало 6 г) на кости выпало 2 (чтобы было понятно, должны выполняться условия и а и в, а вероятность - отношение нужного исхода ко всем возможным) p= 1/6 для всех случаев

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS