Геометрия: В равностороннем треугольнике ABC со стороной 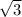проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.

DIMONSTERUSp

07.03.2021 05:51

Геометрия

Есть ответ 👍

В равностороннем треугольнике ABC со стороной $\sqrt{3}$ проведены три биссектрисы AN, BH и CM. Найдите периметр треугольника ALH.

201

269

Посмотреть ответы 2

Ответы на вопрос:

lida20171

Геометрия

4,6(30 оценок)

В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.

- - -

Дано :

ΔАВС - правильный (равносторонний).

АВ = √3.

АМ, ВН, СК - биссектрисы.

АМ ∩ ВН ∩ СК = L.

Найти :

Р(ΔALH) = ?

АВ = ВС = АС = √3 (по определению равностороннего треугольника).

В правильном треугольнике все его биссектрисы являются медианами и высотами.

Соответственно, по определению медианы треугольника -

АН = НС = 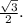$\frac{\sqrt{3} }{2}.$

Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).

В равностороннем треугольнике все углы равны по 60°.

То есть ∠А = 60°.

По определению биссектрисы треугольника -

∠ВАМ = ∠МАС = 60°/2 = 30°.

По определению косинуса острого угла прямоугольного треугольника -

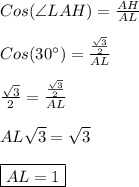
$Cos(\angle LAH) = \frac{AH}{AL}\\\\Cos(30^{\circ} ) = \frac{\frac{\sqrt{3} }{2} }{AL} \\\\\ \frac{\sqrt{3} }{2} = \frac{\frac{\sqrt{3} }{2} }{AL}\\\\AL\sqrt{3} = \sqrt{3} \\\\\boxed{AL = 1}$

В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузе.

Отсюда -

LH = 0,5*AL = 1*0,5 = 0,5.

Периметр - это сумма длин всех сторон.

Отсюда -

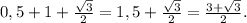
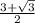Р(ΔALH) = LH + AL + AH = $0,5 + 1 + \frac{\sqrt{3} }{2} = 1,5 + \frac{\sqrt{3} }{2} = \frac{3+\sqrt{3} }{2}.$

$\frac{3+\sqrt{3} }{2}$ (ед).

vorontsovaksus

Геометрия

4,6(23 оценок)

ответ:образуется прямоугольный прямоугольник ABK. Сторона АВ равна 70 см

Объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.