Регистрация Спросить otvet5GPT
bezin2000
10.11.2020 17:58
Алгебра
Есть ответ 👍

решить с раскрытым ответом! Профиль математика

246
410
Посмотреть ответы 2

Ответы на вопрос:

GanDyrAS
GanDyrAS
4,7(48 оценок)

9

Объяснение:

Так как числа образуют арифметическую прогрессию, их можно представить как 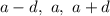a-d,\ a,\ a+d. Их квадраты образуют геометрическую прогрессию. По характеристическому свойству геометрической прогрессии:

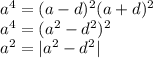
a^4=(a-d)^2(a+d)^2\\a^4=(a^2-d^2)^2\\a^2=|a^2-d^2|

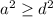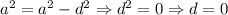Если a^2\geq d^2, то a^2=a^2-d^2\Rightarrow d^2=0\Rightarrow d=0, но тогда все числа равны, что невозможно по условию. Тогда a^2:

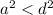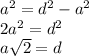
a^2=d^2-a^2\\2a^2=d^2\\a\sqrt{2}=d

Тогда первые два числа арифметической прогрессии равны 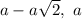a-a\sqrt{2},\ a, геометрической прогрессии — 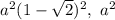a^2(1-\sqrt{2})^2,\ a^2, знаменатель прогрессии —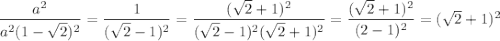 \dfrac{a^2}{a^2(1-\sqrt{2})^2}=\dfrac{1}{(\sqrt{2}-1)^2}=\dfrac{(\sqrt{2}+1)^2}{(\sqrt{2}-1)^2(\sqrt{2}+1)^2}=\dfrac{(\sqrt{2}+1)^2}{(2-1)^2}=(\sqrt{2}+1)^2

Значение данного выражения:

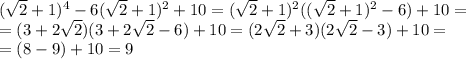
(\sqrt{2}+1)^4-6(\sqrt{2}+1)^2+10=(\sqrt{2}+1)^2((\sqrt{2}+1)^2-6)+10=\\=(3+2\sqrt{2})(3+2\sqrt{2}-6)+10=(2\sqrt{2}+3)(2\sqrt{2}-3)+10=\\=(8-9)+10=9

AndreyVisaGold
AndreyVisaGold
4,6(4 оценок)
Формула прогрессии: b(n)=b(1)*q^(n-1) находишь b(1): b(4)=b(1)*q^(4-1) b(1)=b(4)/q^3 b(1)=4/4^3 b(1)=0,0625 b(6)=b(1)*q^(6-1) b(6)=b(1)*q^5 b(6)=0,0625*4^5 b(6)=64

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS