Алгебра: Докажите, что число 1+1/2+1/3+...+1/m не целое

nastyakholod92

31.07.2020 09:32

Алгебра

Есть ответ 👍

Докажите, что число 1+1/2+1/3+...+1/m не целое

281

282

Посмотреть ответы 2

Ответы на вопрос:

жанара28

Алгебра

4,5(92 оценок)

Пусть сумма ряда :

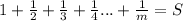
$1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} ...+\frac{1}{m} =S$

Предположим, что число 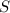- целое число и $m\geq2$

Найдем среди чисел от 1 до m наибольшую степень двойки, то есть такую, что : 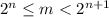$2^n\leq m$ , где 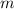- натуральное число.

Умножим обе части равенства на 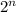2^n :

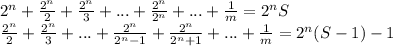
$2^n +\frac{2^n}{2} +\frac{2^n}{3} +...+\frac{2^n}{2^n} +...+\frac{1}{m} =2^nS\\\frac{2^n}{2} +\frac{2^n}{3} +...+\frac{2^n}{2^n -1}+\frac{2^n}{2^n +1} +...+\frac{1}{m} = 2^n(S-1) - 1$

Поскольку число 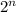2^n имеет максимальную степень двойки для чисел от 1 по m, то все степени двоек входящие в разложение на простые множители чисел от 1 по m, если таковые существуют, сократятся c числителем

- натуральное нечетное число.

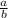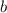Приведем все дроби к наименьшему общему знаменателю, но поскольку, наименьший общий знаменатель нечетных чисел число нечетное, а все числители четные, то левая часть равенства будет выглядить так : $\frac{a}{b}$ , где - четное число, - нечетное число.

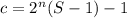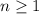Целое число: c=2^n(S-1) - 1 является нечетным при $n\geq1$ .

Тогда : 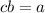cb=a произведение двух нечетных числе число нечетное, но число - четное .

То есть мы пришли к противоречию, а значит число 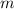- нецелое.

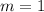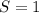Если же m=1 , то S= 1 - целое число.

Примечание: данное доказательство работает не только для данного ряда, но и для любого упорядоченного ряда вида :

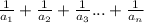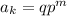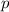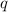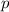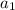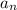$\frac{1}{a_{1} } + \frac{1}{a_{2} } +\frac{1}{a_{3} }...+\frac{1}{a_{n} }$ , если в этом ряду существует число вида $a_{k} =qp^m$ ,где - простое, не делится на , причем в разложении на простые множители каждого из чисел от $a_{1}$ до $a_{n}$ содержится не более чем m-1 - я cтепень числа 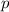, за исключением самого числа 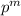p^m . То есть умножаем обе части на 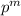p^m и также рассуждаем про делимость на .

ShahTV

Алгебра

4,7(39 оценок)

Объяснение:

переписуй крім закреслених цифер

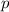Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.