Регистрация Спросить otvet5GPT
navimarik
21.01.2023 13:11
Математика
Есть ответ 👍

с решением уравнения)

277
480
Посмотреть ответы 2

Ответы на вопрос:

Kreizanova
Kreizanova
4,6(4 оценок)

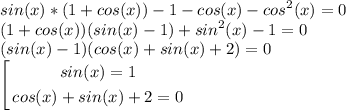
\displaystyle sin(x)*(1+cos(x))-1-cos(x)-cos^2(x)=0\\(1+cos(x))(sin(x)-1)+sin^2(x)-1=0\\(sin(x)-1)(cos(x)+sin(x)+2)=0\\\left[\begin{gathered}sin(x)=1\\cos(x)+sin(x)+2=0\end{gathered}

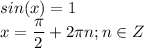
\displaystyle sin(x)=1\\x=\frac{\pi}{2}+2\pi n;n\in Z

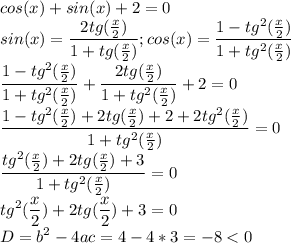
\displaystyle cos(x)+sin(x)+2=0\\sin(x)=\frac{2tg(\frac{x}{2})}{1+tg(\frac{x}{2})};cos(x)=\frac{1-tg^2(\frac{x}{2})}{1+tg^2(\frac{x}{2})}\\\frac{1-tg^2(\frac{x}{2})}{1+tg^2(\frac{x}{2})}+\frac{2tg(\frac{x}{2})}{1+tg^2(\frac{x}{2})}+2=0\\\frac{1-tg^2(\frac{x}{2})+2tg(\frac{x}{2})+2+2tg^2(\frac{x}{2})}{1+tg^2(\frac{x}{2})}=0\\\frac{tg^2(\frac{x}{2})+2tg(\frac{x}{2})+3}{1+tg^2(\frac{x}{2})}=0\\tg^2(\frac{x}{2})+2tg(\frac{x}{2})+3=0\\D=b^2-4ac=4-4*3=-8

Решений нет.

Другой вариант решения данного уравнения: видно что уравнение возможно если:

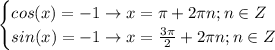
\displaystyle \begin{cases}cos(x)=-1\to x=\pi+2\pi n;n\in Z\\sin(x)=-1\to x=\frac{3\pi}{2}+2\pi n;n\in Z\end{cases}

Однако, как видно, нет таких х, при которых одновременно и sin(x) и cos(x) равны -1.

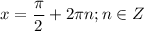
\displaystyle x=\frac{\pi}{2}+2\pi n;n\in Z

AkLeAfAr
AkLeAfAr
4,6(26 оценок)
3,5*2=7 км пройдет 1 турист 4,2*2=8,4 км пройдет 2 турист 8,4-7=1,4 км будет между туристами через 2 часа

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS